Applied stochastic models in business and industry. Trend estimation of financial time series, страница 4

There is a strong connection between the ES filter and the so-called scatterplot smoothing technique employed within the context of semiparametric models (see Ruppert et al. [12] for a thorough discussion of this subject). One of such techniques is penalized splines, which may be deemed as an extension of linear regression modeling and produces smooth curves by way of a smoothing parameter , as with the ES filter. In that context, we can find a mixed model representation of the penalized spline that could lead us to use Kalman filtering for computations and to select via Maximum Likelihood (or else use some other approaches, as generalized cross-validation or Akaike’s information criterion). In what follows, we propose to select with a different approach that comes out by defining first an index of relative precision attributable to smoothness. We prefer this approach over the former ones because this way we have control on the amount of smoothness to be achieved by the trend and this fact allows us to establish more valid comparisons among trends.

To use the ES filter in practice it is essential to choose the value of the smoothing constant () that determines the behavior of the trend completely. The selection of that constant cannot be taken lightly because both smoothness and fit of the trend will depend on its value. In fact, selection of must take into consideration the number of data points available and the frequency of observations. Thus, let us suppose that Equations (7) are true, with {_t} and {_t} two uncorrelated zero-mean white noise processes, with variances ² and ², respectively. In matrix terms we have

                                                 Y=s+g with E(g)=0,              Var(g)=²I_N                                                               (12)

and

                                               K_1Ns=e with E                                    (13)

Now, since E 0, we get

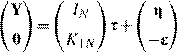
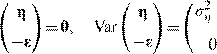
IN

with E(14)

Therefore, as did Guerrero [10] with the HP filter, we use generalized least squares to produce the linear estimator with minimum MSE, given by

                                                  sˆY                                        (15)

For this result to be completely equivalent to that provided by the WK filter, we also assume that the initial value of {Y_t} is independent of g and e. By looking at the precision matrix −¹, we see that it is the sum of two precision matrices, −²I_N corresponding to model (12) and − ²K_{1 N} K_1N associated with (13). To measure the proportion of P in (P+Q)−¹, where P and Q are N ×N positive definite matrices, we will use the index proposed in Guerrero [9, 10]. Such an index is

                                                           (P; P+Q)=tr[P(P+Q)−¹]/N                                               (17)

where tr(.) denotes trace of a matrix. This index has the following properties: (i) it takes on values between zero and one, (ii) it is invariant under linear nonsingular transformations of the variable involved, (iii) it behaves linearly and (iv) it is symmetric, in the sense that (P; P+Q)+

(Q; P+Q)=1.

Thus, we use (17) to quantify the proportion of precision attributable to trend smoothness induced by (13). It is considered as an index of relative precision contributed by the smoothing model and its expression becomes

S(; N) = (− ²K_{1 N} K_1N;)

                                                                      = 1−tr[(I_N +K_{1 N} K_1N)−¹]/N                                       (18)

with =²/². This index depends only on the values of and N because the matrix K_1N is fixed. It is clear that S(; N)→0 when →0 and S(; N)→1 when →∞. For convenience, we will use the notation 100S(; N)% or simply S%, to interpret it as a percentage of smoothness achieved by the ES filter.