Theorem 12. The competitive ratio of Algorithm DELAY for instances with customer locations on the non-negative real line is 2 for any length T of the planning horizon.
Proof. Similar to the proof of Theorem 11. ■
Finally, we turn to the performance analysis of SMART(p). We consider the case T = 3. We start by examiningoptimaloff-linealgorithms.Whentheplanninghorizon has three time periods, there are two decision points, since in the third time period we have to serve all remaining customers. Let i denote the decision to immediately serve all available customers, and let d denote the decision to delay all customers that can be postponed. Let the sequence id denote an algorithm that applies IMMEDIATE on the first day and DELAY on the second day. Similarly we define the other decision sequences ii, di, and dd.
Theorem 13. The off-line optimal solution z∗(I) for instances I with customers on the non-negative real line and a planning horizon of three time periods is given either by z(id,I) or z(di,I). Moreover, z(di,I) < z(id,I) if and only if L1 + L3 < min(L1|2,L2|3).
Proof. The decision sequences ii and dd are dominated by id, since z(ii,I) = L1,1|2 + L2|3 + L3 ≥ L1,1|2 + L2|3,3 = z(id,I) and
z(dd,I) = L1 + L1|2 + L2|3,3 ≥ L1,1|2 + L2|3,3 = z(id,I).
To prove the second part of the theorem, observe that z(id,I) = L1,1|2 + L2|3,3 = max(L1,L1|2) + max(L2|3,L3) and z(di,I) = L1 + L1|2,2|3 + L3 = L1 + max(L1|2,L2|3) + L3.
We compare the two non-dominated decision sequences by analyzing a number of cases:
• If L1 ≥ L1|2 and L3 ≥ L2|3, then z(id,I) ≤ z(di,I) because z(id,I) = L1 + L3 ≤ L1 + max(L1|2,L2|3)+ L3 = z(di,I).
• If L1 ≥ L1|2 and L3 < L2|3, then z(id,I) ≤ z(di,I) because z(id,I) = L1 + L2|3 ≤ L1 + max(L1|2,L2|3)+ L3 = z(di,I).
• If L1 < L1|2 and L3 ≥ L2|3, then z(id,I) ≤ z(di,I) because z(id,I) = L1|2 + L3 ≤ L1 + max(L1|2,L2|3)+ L3 = z(di,I).
• If L1 < L1|2 and L3 < L2|3, then z(id,I) ≤ z(di,I) if and only if min(L1|2,L2|3) ≤ L1 + L3 because z(id,I) = L1|2 + L2|3 ≤ L1 + max(L1|2,L2|3)+ L3 = z(di,I) ⇔ min(L1|2,L2|3) ≤ L1 + L3.
We conclude that z∗(I) = z(di,I) < z(id,I) if and only if
L1 + L3 < min(L1|2,L2|3). ■
Theorem 14. The competitive ratio of Algorithm
SMART(p) for instances with
customers on the non-negative real line and a planning horizon of three time
periods is 
p+p p , with a best ratio of 
for
p = 2.
Proof. The performance of SMART(p) can be analyzed by studying its three possible decision sequences. There are only three decision sequences that need to be analyzed, because the decision sequence ii will never be applied by SMART.
Case dd. SMART(p) applies dd under the following conditions:
L1L|21,,21||23 >> pLpL11|2 that imply 
| | 1p2L1.
Since p > 1, the inequality L1 < L1|2 < L2|3 holds. For the case z(id,I) ≤ z(di,I), the ratio is
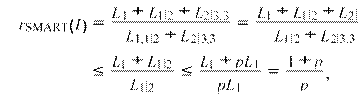
while for the case z(di,I) < z(id,I), the ratio is
rSMART
< L1 + L1|2 + L2|3 < L1 + L1|2 + pL1|2
L1
+ L2|3 L1
+ pL1|2
L1
< |2 + pL1|2 < 1 + p.
pL1|2 p
Therefore,
1 
+ p
rSMART(I).
p
Case di. SMART(p) applies di under the following conditions:
L1,1 2 > pL1L1
that imply
L1|2,2|3 ≤ pL1|2 | | .
If z∗(I) = z(di,I), then rSMART(I) = 1. Thus, we consider the case for which the off-line optimum is z∗(I) = z(id,I) and the ratio is
2
3,3 rSMART(I) 
.
If L2|3 < L1|2, then rSMART(I) ≤ L1 + L1+|2 + L2|3,3 ≤ L1 + L1|2 < 1 +
p.
L1|2 L2|3,3 L1|2 p
|
Therefore, |
L1|2 pL1|2 pL1 p2L1 p p2 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
≤
L1 ++2pL1|2 ≤ L1 ++2p2L1 ≤ 1 ++2p2 .