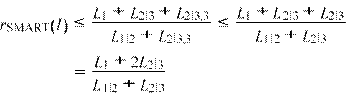Competitive Analysis for Dynamic Multiperiod. Uncapacitated Routing Problems Enrico Angelelli and M. Grazia Speranza, страница 10

If L₁|2 < L₂|3, then

      rSMART            .

Case id. SMART(p) applies id under the following condition:

L_1,1|2 ≤ pL₁ that implies L₁|2 < pL₁.

If z∗(I) = z(id,I), then r_SMART(I) = 1. Thus, we consider the case for which the off-line optimum is z∗(I) = z(di,I). By Theorem 13 we assume L₁ + L₃ < min(L₁|2,L₂|3) and the ratio is bounded as follows r_SMART(I)

       ⁼        +     L1|2 + L2|3                    ^≤        +L1|2 + L2|3

            L₁         max(L₁|2,L₂|3) + L₃           L₁       max(L₁|2,L₂|3)

≤ min(L1|2,L2|3) + max(L1|2,L2|3)

L₁ + max(L₁|2,L₂|3)

≤ 2+min(L1|²,L2|³) _< 2+pL1 = 2+p _. L₁ min(L₁|2,L₂|3) L₁ pL₁ 1 p

The latter inequality comes from min(L₁|2,L₂|3) ≤ L₁|2 < pL₁.

Combining these results, we obtain

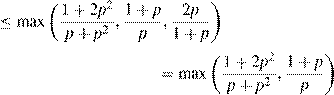rSMART

.

The minimum upper bound on the competitive ratio is attained for p = 2 for which SMART(p) guarantees a worstcase ratio less or equal to .

Toshowthattheboundistight,considerthefollowingtwo instances:

1.  LetC₁ containasinglecustomeratdistance1,C_1|2 asingle customer at distance p +ε, and let C_2|3 = C₃ =∅. Then, SMART(p) visits C₁ in the first time period and C_1|2 in the second time period. The ratio is , which can be

arbitrarily close to 1+pp. Thus, rSMART(p) ≥ 1+pp.

2.  Let C₁ contain a single customer at distance 1, C_1|2 a single customer at distance ^p+ε, and C_2|3 and C₃ a single customer at distance p². Then, SMART(p) visits C₁ in the first time period, C_1|2 and C_2|3 in the second time period,2 and C₃ in the last time period. The ratio is _p¹+⁺_ε²+^p_p2 , which

1

          canbearbitrarilycloseto p+p . Thus,r_{SMART(p)               p}+_p .

        Therefore, for any p        >        1, we have r_SMART            =

                              . Its minimum value isfor p        2.            ■

           _p+p                                               _p=

4.3. A Time-Dependent Variant of Algorithm SMART

For instances with a planning horizon of three time periods, we have established a lower bound on the competitive ratio of any algorithm of 1.44 and a competitive ratio for SMART. It may still be the case that SMART(2) is an optimal algorithm. Unfortunately, the following theorem shows that a version of SMART with time-dependent parameters achieves a better competitive ratio than SMART(2). Consider SMART(p₁,p₂), which applies SMART(p₁) in the first time period and SMART(p₂) in the second time period.

Theorem 15. The competitive ratio of Algorithm SMART(p₁,p₂) for instances with customers on the nonnegative real line is , with a best ratio of 1.473 for p ₂

Proof. With arguments similar to those in the proof of Theorem 14, we find that

rSMART(p₁,p₂) ≤ β(p1,p2)

,

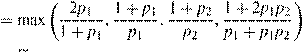rSMART(p.

We make the following observations:

• ¹⁺_p2^p2 is decreasing with p₂ for any p₁; • ¹⁺1 ²_p^p1¹_p^p2² is increasing with p₂ for any p₁. _p +

To minimize β, p₂ should be taken such that ¹⁺_p2^p2 =

1

p , that is p                                       . Thus, we consider

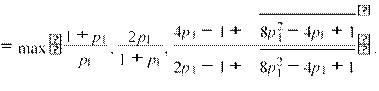
β(p₁) = β(p₁,p₂(p₁))

formance is r_SMART  1.473, for p₁  2.79 and The minimum is attained at2.79. The guaranteed perp₂  2.11.

The tightness of this bound can be proved with an argument similar to the one used in Theorem 14. ■ Inthissection,wehaveestablishedthatalgorithmsIMMEDIATE and DELAY have a competitive ratio of 2 independently of the length of the planning horizon, but that the competitive ratio of SMART(p) increases when we increase

the length of the planning horizon to T = 3 and that it is no longer optimal.

The lower bound obtained for the non-negative real line clearly holds for Euclidean instances as well. The extension oftheanalysisofIMMEDIATEandDELAYtotheEuclidean plane is straightforward and gives the same competitive ratio.

5.  FUTURE RESEARCH

We have studied a dynamic multiperiod routing problem and have analyzed three simple algorithms for its solution, i.e.,IMMEDIATE,DELAY,andSMART(p).Wehaveshown that SMART(p), with an appropriate parameter p, outperforms IMMEDIATE and DELAY on instances with short planning horizons.