Competitive Analysis for Dynamic Multiperiod. Uncapacitated Routing Problems Enrico Angelelli and M. Grazia Speranza, страница 8

4.1. A Lower Bound

The next theorem shows that for planning horizons with more than two time periods, the lower bound on the compet-√

itive ratio of any algorithm is strictly greater than    2.

Theorem 10. The competitive ratio of any algorithm for DMPRP with a planning horizon T > 2 and with customer locations on the non-negative real line is greater than or equal to 1.44.

Proof. Consider the following instance with three time periods, T = 3. The customer set C₁ contains a single customer at distance 1 from the depot (located at the origin) and the customer set C₁|2 contains a single customer at distance a > 1 from the depot.

First, we consider algorithm A of the class of algorithms that at the beginning of the first time period decide to visit the customers in C₁ and C₁|2. Now assume that the customer set C₂|3 contains a single customer at distance a from the depot and that C₃ = ∅. Then, z2a, while the off-line optimum is z∗(I) = 2 + 2a. Thus, r_{A a}.

Next, we consider algorithm A of the class of algorithms that at the beginning of the first time period decide to visit only the customers in C₁. Now assume that the customer set

Cdepot. If algorithm2|3 contains a customer at distanceA at the beginning of the second timeab, with b > 1, from the

period decides to visit the customers in C₁|2 and C₂|3, then assume that C₃ contains a customer at distance ab. Then, z = 2 + 2ab + 2ab, while the off-line optimum is

zbeginning of the second time period decides to visit only the∗(I⁾ = 2a + 2ab. Thus, r_A ≥ ¹_a⁺+²_ab^ab. If algorithm A at the 2customers in+2a+2ab, while the off-line optimum isC¹|², then assume that C³ = ∅ z∗_(I) = ₂+_2ab.

Thus,Consequently, for any algorithmrA ≥ 1+1+a+abab.  A we have

               r_A  .          (3)

We want to establish the maximum lower bound (3). Suppose thata isfixedandfocusonthelasttwotermsoftheminimum. Since the first of these is an increasing function of b while the last is a decreasing function of b, the maximum value of the minimum of these two terms is attained at equality, i.e., when

1 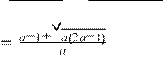 ++2ab = 1 ++a + ab

, a  ab           1             ab

which implies b                            . Therefore,

rA .

The first term is an increasing function of a and the second term is a decreasing function of a. Therefore, the maximum value of the lower bound (3) is attained at a  2.575 (with b  1.881) and its value is approximately 1.44. Thus, r_A ≥

1.44.                                                                                          ■

4.2. Analysis of Algorithms

Next, we turn our attention to the performance of algorithms IMMEDIATE and DELAY.

Theorem 11. The competitive ratio of Algorithm IMMEDIATE for instances with customer locations on the nonnegative real line is 2 for any length of the planning horizon.

Proof. Assume T is even. (The case T is odd is handled similarly.) Let I be an instance for which the maximum ratio z(IMMEDIATE,z∗(I) I) is attained. It is easy to see that z(IMMEDIATE,I) = L_1,1|2 + L₂|3 + ... + L_T−1|T + L_T.

Next, consider an optimal solution. In an optimal solution all customers in C₁|2 have to be served in time periods 1 and 2. Therefore, the cost incurred in an optimal solution over time periods 1 and 2 is at least L₁|2. More generally, for t even, all customers in C_t−1|t have to be served in time periods t − 1 and t in an optimal solution. Therefore, the cost incurred in an optimal solution over time periods t − 1 and t is at least

L_t−1|t. Consequently, z∗(I) ≥ L1|2 + L3|4 + ··· + LT−1|T.

Analogously, for t odd (t ≥ 3), all customers in C_t−1|t have to be served in time periods t−1 and t in an optimal solution. Since an optimal solution also incurs a cost of at least L₁ in the first time period and at least L_T in the last time period, we find that

z∗(I) ≥ L1 + L2|3 + ··· + LT−2|T−1 + LT.

Combining these two observations we find

2^z∗(I) ≥ L1,1|2 + L2|3 + ··· + LT−2|T−1 + LT−1|T + LT.

This shows that Algorithm IMMEDIATE never incurs a cost that is more than twice that of an optimal solution. ■