Competitive Analysis for Dynamic Multiperiod. Uncapacitated Routing Problems Enrico Angelelli and M. Grazia Speranza, страница 7

(OABO and OACO). The optimal off-line solution has cost CO plus OA  BO). The ratio tends to tends to 0.

As observed earlier, no other partition of the customer sets can lead to a better solution. Therefore, any algorithm has a competitive ratio greater than or equal to . ■

Next, we analyze the performance of the algorithms IMMEDIATE and DELAY when applied to Euclidean instances.

Theorem 7. The competitive ratio of Algorithm IMMEDIATE for Euclidean instances is 2 and the bound is tight.

     Proof.    Same argument as Theorem 2.                           ■

Theorem 8. The competitive ratio of Algorithm DELAY for Euclidean instances is 2 and the bound is tight.

     Proof.    Same argument as Theorem 3.                           ■

Next, we analyze the performance of algorithm SMART(p) on Euclidean instances when p = 2.

Theorem 9. The competitive ratio of Algorithm SMART(2) for Euclidean instances is . The algorithm is optimal.

Proof. The optimal solution for any instance partitions thecustomersinC₁|2 intotwosets,thesetofcustomersvisited inthefirsttimeperiod,C₍₁|2_)a,andthesetofcustomersvisited in the second time period, C₍₁|2_)b.

As before, we denote by L₍₁|2_)a and L₍₁|2_)b the length of an optimal tour starting and ending at the depot and visitsimilar way, we defineing all customers in CL(1₁|2_,()₁a|2₎and_a andC(L1|₂2_,)₍b₁, respectively. In a|2_)b so that z∗_(I) =

L_1,(1|2_)a +L_2,(1|2_)b. Furthermore, let M = max(L₂,L₍₁|2_)b) ≤ L_2,(1|2_)b. Observe that from the triangle inequality we have the following inequalities

L1,1|2 ≤ L1,(1|2)a + L(1|2)b ≤ L1,(1|2)a + M (1) z∗(I) ≥ L_1,(1|2_)a + M ≥ L₁ + M.        (2) If L_1,1|2 ≤ 2L₁, then Algorithm IMMEDIATE is applied and, from (1) and (2), we derive

L1,1

     rSMART(I) =                |2 + L2             ≤ L1,(1|2)a + M+ + L2

                            L1,(1|2)a + L2,(1|2)b                L1,(1|2)a       M

≤ L1,(1|2)a + 2M

L1,(1|2)a + M

≤ L¹ ++2M = 1 ++2(M/L1)

.

                             L₁       M         1      (M/L₁)

Moreover, from L_1,1|2 ≤ 2L₁ and (2), we derive

≤  .

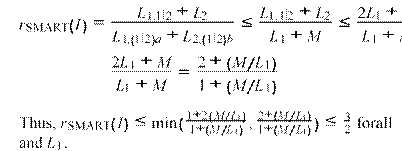If L1,1|2 > 2L1, then Algorithm DELAY is applied and from z∗(I) ≥ Lall ≥ max(L1,1|2,L1|2,2), we obtain

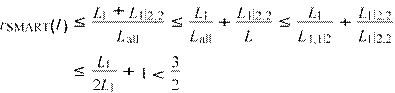all

.

In conclusion, we have r_SMART(I⁾ ≤ ₂³ for all instances I.

Thus, r_SMART  when p = 2. The tightness of the bound andtheoptimalityofthealgorithmcomefromTheorem6. ■

Observe that Algorithm SMART(p) either serves all customers in C₁|2 in the first time period, when Algorithm IMMEDIATE is selected, or serves all customers in C₁|2 in the second time period, when Algorithm DELAY is selected. This is an algorithmic choice. The DMPRP, as defined in Section 2, does allow customers in C₁|2 to be split over the first and second time period.

4.  DYNAMIC MULTIPERIOD ROUTINGPROBLEM—GENERAL CASE

The algorithms defined in Section 3 naturally extend to a planning horizon with more than two periods: apply the same decision rule at the beginning of each time period, i.e., at the beginning of time periods 1,2,...,T −1 for a planning horizon with T periods, since no decision has to be made at the beginning of the last period (all remaining orders have to be delivered).

In this section, we provide a lower bound on the competitive ratio of any online algorithm for DMPRP with a planning horizon T > 2, we establish the competitive ratio of AlgorithmIMMEDIATEandAlgorithmDELAYforthecase T > 2, and we show that Algorithm SMART(p) is no longer optimal for the case T > 2, as a variant in which the parameter p is changed from time period to time period already outperforms SMART(p) for the case T = 3. We restrict the analysis to instances with customers on the non-negative real line.

Let L₁ denote the length of the tour that visits only customers in C₁, let L_T denote the length of the tour that visits only customers in C_T, and let L_t−1|t denote the length of the tour that visits only customers C_t−1|t for t = 2,3,...,T. Finally, let L_t−1|t_,t|t+1 denote the length of the optimal merge of the tours L_t−1|t and L_t|t+1, for 2 ≤ t ≤ T − 1. Let L_1,1|2 denotetheoptimalmergeofthetoursL₁ andL₁|2 andL_T−1|T_,T the optimal merge of the tours L_T−1|T and L_T.