Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 7

Определение. Прямые, перпендикулярные фокальной оси эллипса (гиперболы) и отстающие от центра на расстояние 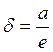, где а – фокальная полуось, а е – эксцентриситет, называются директрисами эллипса (гиперболы).

Если эллипс (гипербола) задан каноническим уравнением, то уравнения директрис таковы:

                                                  (4.6.1)

Директрисы показаны на рис. 4.23 и 4.24, их обозначения d₁ и d₂ соответствуют обозначениям фокусов F₁ и F₂. Заметим, что в случае эллипса , так как эксцентриситет эллипса меньше 1, а для гиперболы , так как ее эксцентриситет больше 1.

Теорема (фокальное свойство эллипса и гиперболы). Отношение фокального радиуса произвольной точки эллипса (гиперболы) к расстоянию от этой точки до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса (гиперболы).

Доказательство. На рис. 4.23 и 4.24 М(х, у) – произвольная точка эллипса (гиперболы), F₁M –ее фокальный радиус относительно первого фокуса, MD – ее расстояние до соответствующей директрисы. Требуется доказать, что

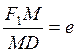                                                        (4.6.2)

в силу симметрии эллипса (гиперболы)относительно оси ординат доказательство достаточно осуществить только для одного фокуса. Подробно мы выполним доказательство только для эллипса, соответствующую выкладку для гиперболы читателю предлагается выполнить самостоятельно.

                    у                                                                 у      

                                                                               d₂                          d₁

                       М      D

                                                                     ·                      о                               ·           x

                 F₂         o        F₁         x                           F₂                                            F₁

                                                                      M                                   D

d₂                        d₁

Рис. 4.23                                                      Рис. 4.24

Пусть F₁(с, 0) – фокус эллипса 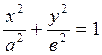. Фокальный радиус произвольной точки эллипса мы вычисляли раньше (формула 4.2.3): . Далее имеем: . Поэтому 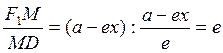, что и требовалось доказать.

Можно доказать и обратное, а именно, что множество точек, характеризующееся условием (4.6.2), есть эллипс при  или гипербола при . При  это условие совпадает с бескоординатным уравнением параболы (4.5.1). Таким образом, эллипс, гипербола и парабола могут быть определены одним бескоординатным уравнением (4.6.2). Значит, указанным трем кривым, назвав их общим термином, можно дать одно определение.

Определение. Пусть дана прямая (директриса) и не лежащая на ней точка (фокус). Множество точек, отношение расстояний от которых до фокуса и до директрисы есть величина постоянная (эксцентриситет), называется невырожденной квадрикой.

На рис. 4.25 показаны три вида невырожденных квадрик. Заметьте, что вершина параболы находится в середине перпендикуляра FP, опущенного из фокуса на директрису, вершина эллипса –ближе к фокусу, а вершина гиперболы – ближе к директрисе (почему?).

§ 4.7. Полярное уравнение невырожденной квадрики

Определение невырожденной квадрики в предыдущем параграфе позволяет легко вывести ее уравнение в полярных координатах.

Фокус F примем за полюс полярной системы координат, а луч FL, перпендикулярный директрисе d и не пересекающий ее, - за полярную ось (рис. 4.26). Если  - произвольная точка квадрики и MD – перпендикуляр, опущенный из этой точки на директрису, то по определению 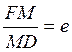, где е – эксцентриситет квадрики.

Так как  и , где р – расстояние от фокуса до директрисы, то уравнение квадрики в полярных координатах таково: .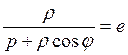

              ветвь гиперболы

        d                                 парабола

                                                                               D                       M