Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 26

                                       Вычислим скалярное произведение  двумя способами. По определению скалярного произведения .

Далее. Обозначив координаты точки D через , имеем  и по формуле (5.2.3)

получаем:

. Но , поэтому

 и, следовательно .

С учетом этого . Приравниваем оба значения скалярного произведения: , откуда 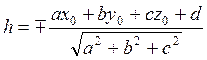. Но так как, то из двух значений надо брать неотрицательное:

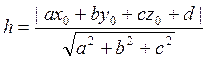                                   (6.4.1)

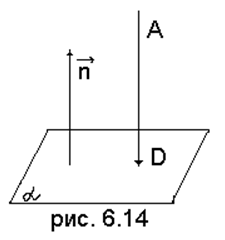
Вывод: расстояние от точки до плоскости равно дроби; в числителе которой стоит абсолютная величина того значения, которое принимает левая часть общего уравенния данной плоскости, если в нее вместо текущих координат подставить координаты данной точки, а в знаменателе – корень квадратный из суммы квадратов коэффициентов при текущих координатах.

Примечание. В планиметрии аналогичную задачу – найти расстояние от точки до прямой – мы решали в § 3.4. Там мы воспользовались другим способом, который можно было бы применить и здесь: найти уравнение прямой AD, затем – D как точку пересечения плоскости с прямой. Тогда искомое расстояние мы нашли бы как расстояние между двумя точками. Но для этого нужно было предварительно рассмотреть уравнение прямой в пространстве. Заметим также, что и в § 3.4 можно было применить более экономический способ этого параграфа.

Пример. Дан тетраэдр с вершинами А(-4, 5, 3), В(-3, 2, 1), С(-2, 1, 3), D(-1, 3, 2). Найдите длину его высоты, опущенной из вершины А.

Эта задача уже решалась с применением векторного  и смешанного произведений векторов в § 5.7.

Решение. Находим уравнение плоскости BCD по точке В и направляющим векторам  и 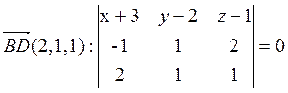. После упрощений получаем . Теперь по формуле (6.4.1) находим длину высоты как расстояние от точки А до плоскости основания: .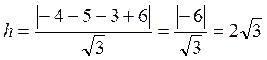

§ 6.5. Пучок и связка плоскостей

Определение. Собстенным пучком плоскостей называется множество плоскостей, проходящих через одну прямую (ось пучка); несобственным – множество параллельных между собой плоскостей.

          Пучки показаны на рис. 6.15 и 6.16.

Пучок, независимо от его вида, определяется любыми

двумя его плоскостями, которые в этом качестве называются образующими

пучками.

Теорема. Пусть имеется пучок с образующими  и. Тогда уравнение

                    (6.5.1)

где λ – переменное, есть уравнение этого пучка без плоскости α₂.

Доказательство этой теоремы совершенно аналогично доказательству теоремы о пучках прямых (§ 3.6), и мы его опускаем.

Как указано в формулировке теоремы, уравнение (6.5.1) описывает пучок с исключенной второй образующей. Полный пучок задаеся уравнением с двумя переменными параметрами λ₁ и λ₂:

                (6.5.2)

В ряде вопросов полезно рассматирвать также связку плоскостей. Так называется множество плоскостей, проходящих через одну фиксированную точку (собственная связка), или параллельных одной фиксированной прямой (несобственная связка). Для определения связуи требуется три образующих

.

Ее уравнение имеет вид

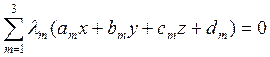                        (6.5.3)

Где  - переменные. Доказательство этого факта опускаем.

Пример 1. В пучке плоскостей с образующими  найдите плоскость, параллельную оси ординат.

Решение. Уравнение пучка имеет вид  или

В уравнении плоскости, параллельной оси ординат, отсутствует член с у (§ 6.2). В данном случае это будет при условии , то есть при . Подставляя это значение λ в уравнение пучка, получаем уравнение искомой плоскости:  или, после сокращения, .

Пример 2. Принадлежит ли плоскость  пучку ?

Решение. Первый способ. Выясним, можно ли подобрать λ так, чтобы из уравнения пучка получить уравнение плоскости α. Представив уравнение пучка в виде , воспользуемся условием (6.3.5) совпадения двух плоскостей: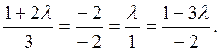

          Мы получили три уравнения с одним неизвестным λ. Если система не разрешима, то плоскость α пучку не принадлежит. Но система разрешима, она имеет решение  Следовательно, плоскость α принадлежит пучку.