Кривые второго порядка (квадрики). Эллипс и его простейшие свойства. Каноническое уравнение эллипса, страница 27

Второй способ. Данный пучок  - собственный, так как его образующие не параллельны. Поэтому плоскость α принадлежит пучку, если она проходит через ось. Отсюда вытекает следующий план решения:

на оси пучка выбрать произвольно две точки А и В, и если окажется, что А, В α, то это будет означать, что плоскость α входит в пучок (рис.6.17).

Точка лежит на оси пучка, если её координаты удовлетворяют уравнениям обеих образующих:

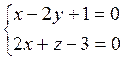
В этой системе неизвестное – свободное, его значение можно взять произвольно.

Пусть , тогда . Таким образом, получается точка А(-1, 0, 5).

Пусть , тогда . Таким образом, получается точка В(1, 1, 1).

Непосредственной проверкой убеждаемся, что . Поэтому плоскость α принадлежит пучку.

§ 6.6. Основные виды уравнений прямой

Как отмечалось в § 5.3, линия в пространстве рассматривается в аналитической геометрии как пересечение двух поверхностей и поэтому задается системой двух уравнений (5.3.5). Прямая задается как линия пересечения двух плоскостей  , для которых выолняется условие непаралельности (6.3.6). Таким образом, прямая  в пространстве определяется системой двух уравнений первой степени:

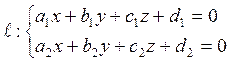                               (6.6.1)

Эти уравнения называются общими уравнениями прямой.

Отметим, что одна и та же прямая может быть задана разными (но равносильными) системами уравнений. Если плоскости α₁ и α₂ рассматривать как образуующие собственного пучка (6.5.2), то прямая  - ось этого пучка. Она может быть задана и двумя любыми другими плоскостями пучка:

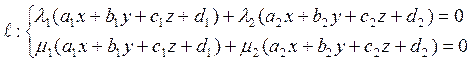 разумеется, пары  и  не должны быть пропорциональными. Например, системы  и 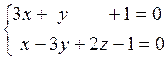, определяют одну и ту же прямую, так как вторая система получается из первой почленным сложением и вычитанием ураавнений, то есть в этом случае. Нам потребуются  и более специальные виды уравнений прямой.

Задача. Найти уравнения прямой  по точке  и направляющему вектору .

Решение. Аналогичная задача для прямой на плоскости решалась в § 3.1.

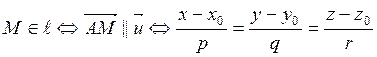Пусть М(х, у, z) – какая-либо точка. Тогда  и . Мы получили уравнения прямой по точке и направляющему вектору, называемые также каноническими:

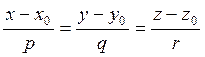                                   (6.6.2)

Заметим, что мы получили систему из двух (подчеркиваем – из двух, а не из трех!) уравнений. Например, таких: 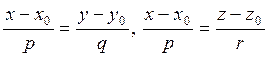. Из полученных уравнений по аналогии с § 3.1 получаем уравнения прямой по двум точкам

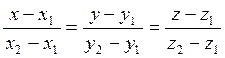                                (6.6.3)

и параметрические уранения прямой:

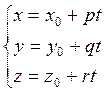                                                    (6.6.4)

Чтобы от общих уравнений прямой перейти к каноническим, надо знать ее точку и направляющий вектор. Для этого достаточно на прямой выбрать произвольно две точки А и В (рис. 6.18) и затем найти уравнение прямой по точке А (или В) и направляющему вектору .

Направляющий вектор прямой  перпендикулярен нормальным векторам  и  плоскостей α₁ и α₂ (рис. 6.19). Поэтому его можно найти и другим способом – по формуле

                                                      (6.6.5)

Пример 1. Найдите уранения прямой по точке А(1, 2, 3) и направляющему вектору .

Решение. Уравнения прямой находим по формуле (6.6.2): 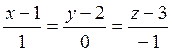 или .

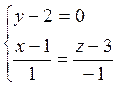Пример 2. Найдите уравнения прямой, по которой плоскость  пересекает плоскость ХОУ.

Решение. Искомая прямая есть линия пересечения двух плоскостей – данной и плоскости ХОУ, уравнение которой z = 0. Поэтому уравнения прямой таковы: 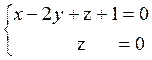 или .

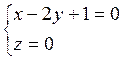Пример 3. Приведите к каноничскому виду уранения прямой .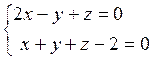

          Решение. Находим на данной прямой две точки А и В. Полагая х = 0, получаем 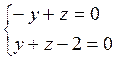, откуда . Итак, А(0, 1, 1). Полагая х=2, получаем 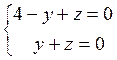, откуда у=2, z=-2. Итак, В(2,2,-2).  Направляющий вектор данной прямой - , поэтому ее канонические уравнения таковы: .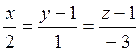

          Пример 4. Найдите направляющий вектор прямой из предыдущего примера.

Решение. При решении примера 3 направляющий вектор был найден. Его можно также найти по формуле (6.6.5): .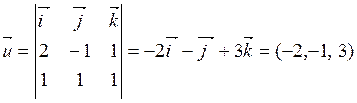

Пример 5. Найдите проекцию прямой 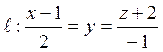 на плоскость .