Оптимальный выбор структуры ГПС в условиях неопределенности развития производства, страница 11

            3. Составление графа переходов. Определение интенсивностей переходов.

3.  Провеpка условий существования стационарного режима.

4.  Составление системы дифференциальных уравнений Колмогорова.

5.  Составление алгебраических уравнений для стационарного   режима.

Постановка задачи. Пусть имеется гибкий производственный модуль, состоящий из двух подсистем ТО и СУ. Потоки отказов и восстановлений ТО и СУ - простейшие. ТО имеет поток отказов  и поток восстановлений . СУ имеет поток отказов и поток восстановлений  , 

Задача заключается в том, чтобы определить вероятности состояний системы и вероятность того, что система "СУ-ТО" работоспособна.

Состояния системы определяются следующим образом:

Е1 - система "СУ-ТО" - работоспособна; (Р/Р)

Е2 - СУ - работоспособна,  ТО - отказало; (О/Р)

Е3 – СУ - отказала,  ТО – работоспособно; (Р/О)

Е4 -  СУ - отказала, ТО – отказало (О/О).

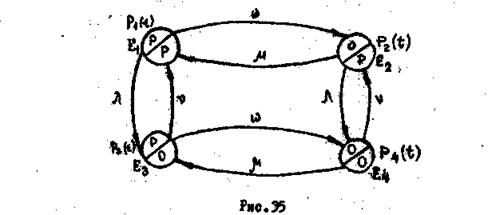
Составление графа переходов (рис. 35) осуществляется расположением на плоскости состояний системы Е1 - Р/Р, Е2 - О/Р, ЕЗ - Р/О, и Е4 - О/О. Каждому состоянию системы соответствуют вероятности нахождения системы в каждом из этих состояний ,  ,  и . Далее фиксируются переходы системы из одного состояния в другое. Например, из состояния Е1 в состояние Е2 система переходит с интенсивности отказов ТО - .  Этот переход представлен стрелкой. Обратный переход осуществляется с интенсивностью .  Аналогично представляются все возможные остальные переходы (рио.35).

Диагональные переходы в графе отсутствует, так как переходы из состояния E1 в состояние Е4 и из состояния Е2 в состояние Е3 связаны о необходимостью происхождения одновременно двух событий (отказов или восстановлений), в то время как в задании указано, что потоки отказов и восстановлений являются простейшими. Судя по графику, система состояний является замкнутой, т.е. из любого состояния есть обратный переход в другое состояние. Это означает, что в замкнутой системе стационарный режим существует всегда.

Следующим этапом является составление дифференциальных уравнений Колмогорова. Для составления первого уравнения рассмотрим изменение вероятности  нахождения системы в состоянии E1. Вероятность нахождения системы в состояний E1 через время   определяется соотношением

 .

Первый член выражения, т.e. , показывает вероятность того, что система, находясь в состоянии E1, за время  не изменит своего состояния. Выражение  - вероятность того, что система, находясь в состоянии Е2, за время   перейдет в состояние E1, а слагаемое   - вероятность перехода системы из состояния Е3 в состояние E1.

Аналогично для состояний Е2 и Е3

 ,

 .

Четвертое уравнение может быть получено из первых трех, следовательно, оно не записывается.

Разделив эти уравнения на  и взяв производную

  ,

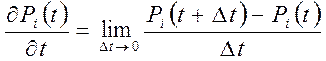получим систему уравнений Колмогорова

  ,

  ,

  ,

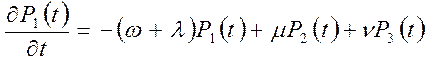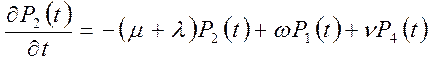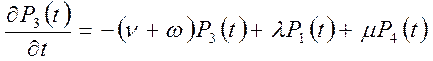 +  +  +  = 1  .

Четвертое уравнение представляет собой условие полной  группы   событий.

Решением системы дифференциальных уравнений являются функции состояний ,  ,  и  - зависимости вероятности соответствующих состояний от времени (рис.36).

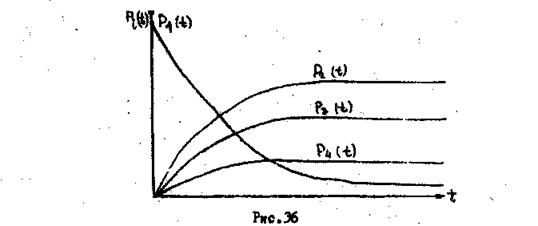
Наличие стационарного режима системы определяется соотношением

 .

При этом производные 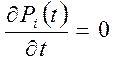  .  В стационарном режиме система дифференциальных уравнения становится системой алгебраических уравнений

  ,

                  ,

                   ,

                     .

Решение системы  - вероятности нахождения системы в соответствующих состояниях. Вероятность   в данном случае имеет вполне определенный смысл - вероятность работоспособного состояния или коэффициент использования системы. Сумма  - представляет собой вероятность неработоспособного состояния системы.

Система дифференциальных уравнений Колмогорова определяет связь между вероятностями нахождения объекта во всех его возможных состояниях. Структура уравнений Колмогорова построена по определенным правилам, позволяющим упростить ее составление.

В левой части каждого уравнения записывается производная вероятности нахождения объекта в рассматриваемом состоянии вершины графа, а правая часть содержит столько членов, сколько ребер графа состояний связано с данной вершиной графа (если ребро направлено из данной вершины, соответствующий член имеет знак минус, если в данную вершин - знак плюс). Каждый член равен произведению параметра потока отказа (восстановления), связанного с данным ребром, на вероятность нахождения в той вершине графа, из которой исходит ребро.

Система уравнений Колмогорове включает столько уравнений, сколько вершин в графе состояния объекта. При этом учитывается условие полной группы событий, т.e.

  .

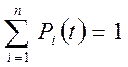6.3. Оценка надежности информационной системы

Рассмотрим трехканальную информационную систему с отказами. Интенсивность потока заявок , интенсивность потока обслуживания .  Возможные состояния системы определяются следующим образом:  

 - все каналы свободны;                                                 

 - занят один канал, два свободных;

- заняты два канала, один свободен;

- заняты все три канала.

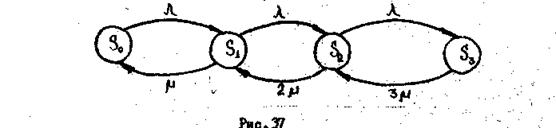
Граф состояний системы представлен на рис.37. Если система находится в состоянии , то поступившая заявка переводит ее в состояние с интенсивностью . Если система находится в состоянии , то   поступившая заявка переводит ее в  с интенси-вностью и т.д.

Переход системы в обратном направлении будет осуществляться при следующих условиях.

Из  (занят один канал) система перейдет в  тогда, когда закончится обслуживание заявки, занимающей этот канал. Интенсивность этого потока событий . Если обслуживанием занято два канала, то поток событий, переводящих систему из  в , будет вдвое интенсивнее, т.е. равен 2. Аналогично поток событий, переводящих
систему из  в , будет равен  3. Пользуясь правилами   п. 8.3, составим систему уравнений Колмогорова для вероятностей состояний системы 

  ,

  ,

  ,

  .

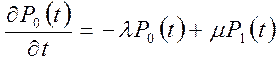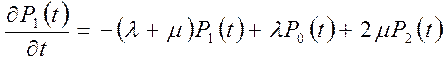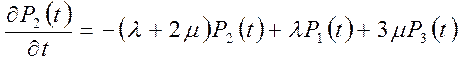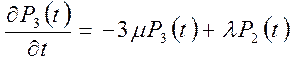Начальные условия (при ): ; .

Решение системы дифференциальных уравнений обычно выполняется на ЭВМ с помощью стандартных программ. При этом будут получены вероятности состояний как функции времени.