Определение коэффициентов
аппроксимации. Оно тесно связано с требуемой точностью. Точность
определяется критериями приближения. Обычно применяют критерии равномерного,
среднеквадратического и интерполяционного (точечного) приближений. Последний
используют наиболее часто. Согласно этому критерию аппроксимируемая функция ![]() и аппроксимирующая функция
и аппроксимирующая функция ![]() (или их производные) должны совпадать в
выбранных (заданных) точках с координатами
(или их производные) должны совпадать в
выбранных (заданных) точках с координатами ![]() (рис. 8.2).
Число таких исходных точек и, следовательно, уравнений, должно быть равным
числу подлежащих определению коэффициентов аппроксимации.
(рис. 8.2).
Число таких исходных точек и, следовательно, уравнений, должно быть равным
числу подлежащих определению коэффициентов аппроксимации.
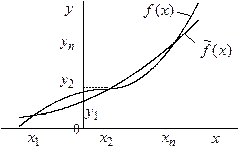
Рис. 8.2
В частности, при аппроксимации степенным полиномом получаем систему уравнений:
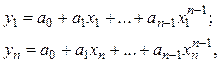 (8.8)
(8.8)
решение
которой и позволит найти коэффициенты ![]() .
.
Для определения коэффициентов аппроксимации можно вводить нелинейные масштабы для приведения заданной зависимости к более простому виду, в частности, к линейному. В последнем случае говорят о методе приведения к линейному виду. После нанесения на график экспериментальных точек в новой системе координат, можно легко установить границы линейной области и, следовательно, правомерность использования принятой аппроксимации; коэффициенты находят по этой области графика. Следует отметить, что нелинейные масштабы можно вводить как по каждой переменной, так и по их комбинации (например, произведению).
Если число заданных точек превышает число определяемых коэффициентов аппроксимации, то можно использовать метод наименьших квадратов, при котором среднеквадратическая ошибка минимальна (см. математические справочники).
Гармонический анализ
Задача анализа
заключается в нахождении гармонических составляющих на выходе НЭ,
аппроксимируемого зависимостью ![]() , при воздействии на его
вход гармонического колебания
, при воздействии на его
вход гармонического колебания ![]() . В этом случае
выходное колебание
. В этом случае
выходное колебание
![]() (8.9)
(8.9)
будет периодической, но
негармонической функцией времени (угла ![]() ),
которую можно представить рядом Фурье
),
которую можно представить рядом Фурье
![]() ,
(8.10)
,
(8.10)
где
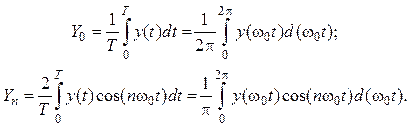 (8.11)
(8.11)
Совершенно аналогично вычисляются синусоидальные составляющие.
Соотношения (8.10) и (8.11) остаются
справедливыми и тогда, когда амплитуда ![]() ,
частота
,
частота ![]() и начальная фаза
и начальная фаза ![]() являются
медленными функциями времени, т. е.
являются
медленными функциями времени, т. е. ![]() ,
, ![]() и
и ![]() , относительные
приращения которых весьма малы за период колебания
, относительные
приращения которых весьма малы за период колебания ![]() , что
важно при рассмотрении амплитудной модуляции, детектирования, преобразования
частоты и др.
, что
важно при рассмотрении амплитудной модуляции, детектирования, преобразования
частоты и др.
Если вычисление интегралов не приводит к громоздким выкладкам, можно пользоваться точными (классическими) формулами (8.11). Однако в целом ряде случаев расчет можно провести значительно проще и быстрее, если воспользоваться другими известными методами, каждый из которых так или иначе базируется на классических формулах (8.11) и является оптимальным для соответствующего вида аппроксимации.
1. Методы с использованием формул трех и пяти ординат. Эти методы применимы как для графических, так и аналитических расчетов. Последнее особенно важно в случае аппроксимации трансцендентными функциями.
Число задаваемых ординат на характеристике НЭ обусловлено числом определяемых составляющих в ряде Фурье (8.10).
Формулы трех ординат служат для
расчета приближенных значений постоянной составляющей ![]() и
амплитуд первой
и
амплитуд первой ![]() и второй
и второй ![]() гармоник
колебания
гармоник
колебания ![]() на выходе НЭ
на выходе НЭ
![]() ,
, ![]() ,
,
![]() (8.12)
(8.12)
по трем
ординатам (рис. 8.3): максимальному ![]() и
минимальному
и
минимальному ![]() значениям и значению
значениям и значению ![]() , которому соответствует отсутствие
гармонического колебания на входе (
, которому соответствует отсутствие
гармонического колебания на входе (![]() ).
).
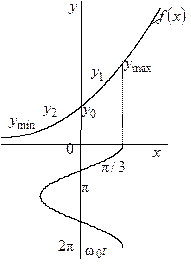
Рис. 8.3
Формулы пяти ординат позволяют
вычислить значения постоянной составляющей ![]() и
амплитуд первых четырех гармоник
и
амплитуд первых четырех гармоник ![]() ,
, ![]() ,
, ![]() ,
, ![]()
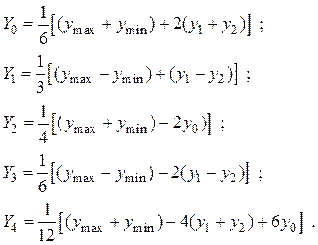 (8.13)
(8.13)
Значения ![]() и
и ![]() соответствуют значениям аргумента (например,
соответствуют значениям аргумента (например,
![]() и
и ![]() ), при
которых входной сигнал равен половине амплитуды.
), при
которых входной сигнал равен половине амплитуды.
2. Метод с использованием тригонометрических формул кратных аргументов. Характеристика НЭ в этом случае аппроксимируется степенным полиномом*
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.