Основные характеристики случайных процессов, страница 4

15. Найдите композицию нормального закона с математическим ожиданием m_x, срединным отклонением  и закона равномерного распределения, заданного на интервале []. Определите относительную ошибку, возникающую от замены суммарного закона нормальным, имеющим то же математическое ожидание и ту же дисперсию. Расчёт произведите для = 0, , ,  в точке  = 0.

4.3.2.  Моментные функции и моменты. Стационарные и эргодические процессы

16. Задан случайный процесс в виде постоянного напряжения случайного уровня , изменяющегося от одной реализации к другой. Можно ли процесс  назвать стационарным и эргодическим?

17. Найдите математическое ожидание, дисперсию и корреляционную функцию процесса

,

где  – случайная величина с известными математическим ожиданием  и дисперсией , а  – детерминированная функция времени. Классифицируйте процесс  по признакам стационарности и эргодичности.

18. Найдите математическое ожидание, дисперсию и корреляционную функцию процесса

,

где  – эргодический случайный процесс с известными математическим ожиданием  и дисперсией  и корреляционной функцией , а  – детерминированная функция. Можно ли процесс  назвать стационарным?

19. Определите математическое ожидание, дисперсию и корреляционную функцию процесса

,

где  и  – некоррелированные стационарные случайные процессы с известными математическими ожиданиями  и , дисперсиями D_x иD_y и корреляционными функциями  и , а  и  – детерминированные функции времени. Стационарен ли процесс ?

20. Задан случайный процесс

,

где  и  – положительные постоянные (амплитуда и частота), а  – случайная величина, равномерно распределённая на отрезке [0, 2p], т. е. . Найдите математическое ожидание и дисперсию, а также классифицируйте процесс по признакам стационарности.

21. Докажите, что процесс , рассмотренный в предыдущей задаче, эргодичен относительно математического ожидания и корреляционной функции. Найдите  и  усреднением по времени.

22. Классифицируйте по признакам стационарности и эргодичности процесс

=,

в котором X(t) – эргодический процесс с известными m_x и D_x, а Y – случайная независимая от времени величина с заданными  и D_y, изменяющаяся от одной реализации к другой.

23. Стационарный случайный процесс X(t) с заданными математическим ожиданием m_x, дисперсией D_x  и одномерной плотностью вероятности  умножили на константу K, например, пропустили через широкополосную линейную цепь с коэффициентом передачи .

Как изменятся указанные параметры случайного процесса?

24. Найдите плотность вероятности, математическое ожидание и дисперсию процесса  вида “телеграфного сигнала”, реализация которого  показана на рис. 4.7.

Вероятность независимых перемен знаков, иначе “опрокидываний” подчиняется закону Пуассона

,

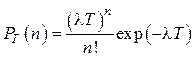где  – среднее число “опрокидываний” в единицу времени,  – вероятность того, что за период произойдёт  “опрокидываний”; при этом .

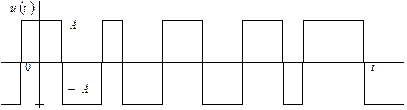
Рис. 4.7

25. Стационарный случайный процесс  имеет функцию распределения , .

Определите математическое ожидание, средний квадрат и дисперсию этого процесса.

26. По данным задачи 10 рассчитайте математическое ожидание, средний квадрат и дисперсию прямоугольного, треугольного и пилообразного колебаний со случайной задержкой.

27. Определите математическое ожидание и дисперсию стационарного случайного процесса, имеющего распределение по закону:

а)

б) .

Коэффициенты  и  также подлежат определению.

28. Плотность вероятности усечённого нормального процесса  имеет вид

 при 0 < < ¥.

Изобразите примерный вид реализации этого процесса и найдите математическое ожидание, средний квадрат, дисперсию и среднеквадратическое значение случайного напряжения.

4.3.3.  Характеристические функции. Энтропия

29. Найдите характеристическую функцию случайной величины X, имеющей плотность вероятности:

а) ;

б) .

30. Покажите, что если закону  соответствует характеристическая функция , то закону  cоответствует характеристическая функция .

31. Используя результаты, полученные в задаче 29, определите математическое ожидание  случайной величины .

32. Найдите характеристическую функцию нормального закона

.

33. Используя результат предыдущей задачи, найдите первые четыре момента нормального распределения.

34. Решите задачу 13 косвенным методом – на основе характеристических функций.

35. Найдите энтропию равномерного закона распределения вероятностей