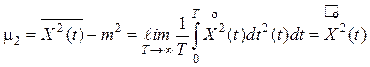Основные характеристики случайных процессов, страница 2

,            (4.13)

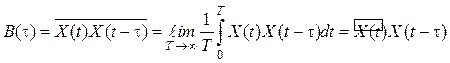,    (4.14)

.                                    (4.15)

Прямая черта означает усреднение по ансамблю реализаций, а волнистая черта – усреднение по времени.

Корреляционные функции обладают следующими основными свойствами:

1.  и , т. е. они чётные.

2. При  эти функции максимальны: , .

3. С ростом  они убывают:  и .

4. При ,  и .

Типичные кривые  и , иллюстрирующие перечисленные свойства, показаны на рис. 4.1, а, б. На рис. 4.1, в дана нормированная корреляционная функция

,                                   (4.16)

обладающая теми же свойствами.

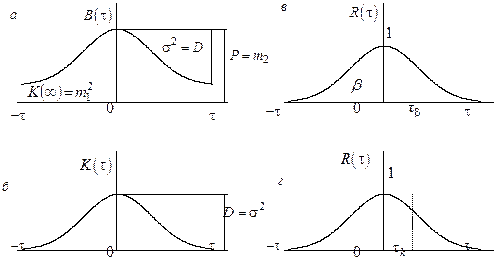
Рис. 4.1

5. Рассмотренные функции убывают не обязательно монотонно. Немонотонность имеет место, например, для процесса, содержащего детерминированную периодическую составляющую.

6. Для случайного процесса, не содержащего детерминированных составляющих, можно указать такой временной интервал, называемый интервалом корреляции , что при  значения  и  практически некоррелированы, т. е. .

Интервал корреляции определяют либо долей  от , либо полушириной основания прямоугольника единичной высоты, площадь которого равна площади под кривой . В первом случае для определения  (рис. 4.1, в) нужно решить уравнение

,                                         (4.17)

а во втором для определения  (рис. 4.1, г) необходимо вычислить интеграл

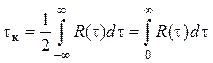.                           (4.18)

При колебательном характере изменения  интервал корреляции определяется координатой  прохождения  через нуль.

Заметим, что равенство  или  нулю ещё не означает независимость случайных величин  и , в то время как независимые случайные величины всегда некоррелированы и для них . Однако для нормального случайного процесса отсутствие корреляции равносильно независимости.

7. Автокорреляционная функция  случайного процесса связана с его спектральной плотностью мощности (СПМ) . Эта связь согласно теореме Винера-Хинчина устанавливается парой преобразований Фурье:

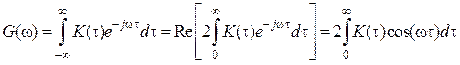,   (4.19)

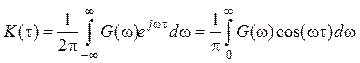.             (4.20)

АКФ и СПМ процессов присущи свойства, которые характерны для любой пары функций, связанных преобразованиями Фурье. В частности, чем уже АКФ, тем шире СПМ  и, наоборот, чем шире АКФ, тем уже СПМ .

Если в качестве меры ширины спектра мощности ввести эффективную (энергетическую) ширину, определяемую основанием равновеликого по площади прямоугольника (на положительной полуоси частот), т. е.

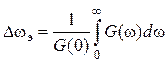,                                (4.21)

то произведение интервала корреляции  на ширину спектра  есть величина постоянная

 и ,                           (4.22)

где .

При суммировании двух случайных процессов, т. е.

,                                   (4.23)

обладающих известными характеристиками, автокорреляционная функция суммы

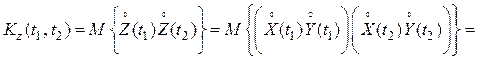
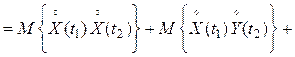
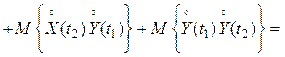
             (4.24)

т. е. равна сумме автокорреляционных функций ,  и так называемых взаимных корреляционных функций (ВКФ)  и  этих процессов.

Случайные процессы называют стационарно связанными, если ВКФ  и  зависят не от самих аргументов  и , а только от разности . В этом случае

.                                   (4.25)

Для статистически независимых процессов , и это означает, что процессы не коррелированы. Обратное утверждение в общем случае несправедливо.

Отметим, что ВКФ не обязательно обладает перечисленными свойствами автокорреляционной функции (АКФ).

Одномерный закон распределения суммарного процесса Z(t) в случае статистически независимых процессов X(t) и Y(t) определится как композиция законов распределения слагаемых, т. е. как свертка

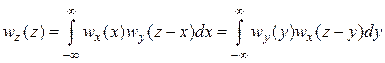;          (4.26)

при этом характеристическая функция q_z (v) равна произведению характеристических функций исходных процессов, т. е.

                                   (4.27)

и

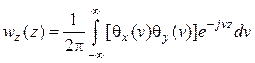.                       (4.28)

С помощью характеристических функций удобно также находить плотность вероятности стационарного случайного процесса, подвергнутого функциональному преобразованию. Так если , то

.                   (4.29)

Наконец, отметим некоторые свойства нормального узкополосного процесса, сформированного, например, из белого шума вырезанием узкой полосы частот и представляющего собой квазигармоническое колебание вида

,                             (4.30)

где  и  – огибающая и начальная фаза – медленные функции по сравнению с .

Одномерная плотность вероятности  огибающей  описывается законом Рэлея:

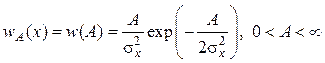,                (4.31)