Основные характеристики случайных процессов, страница 3

при этом  и .

Начальная фаза этого процесса распределена равномерно

.                             (4.32)

В заключение приведём условную схему (граф) основных характеристик случайного процесса (рис. 4.2.) Каждая из стрелок на схеме указывает на возможность перехода от одной характеристики к другой путём математического преобразования; знак “ò” означает интегральное преобразование, знак “(.)' “ указывает на производную, ПФ – преобразования Фурье.

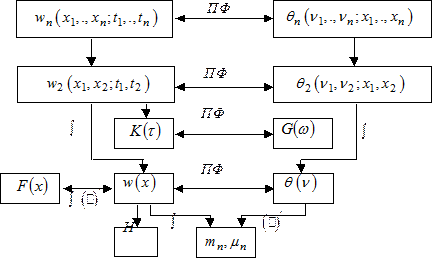
 Рис. 4.2

4.3. Задачи

4.3.1. Вероятностные характеристики

1. Случайный процесс  в фиксированный момент времени определяется одномерной плотностью вероятности вида

 при x > 0.

Установите связь между параметрами  и b.

2. Задан одномерный интегральный закон распределения вероятностей случайного процесса

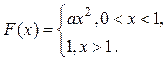
Найдите значение параметра , плотность вероятности , а затем вероятность того, что случайная переменная  будет лежать в интервале от  до , причём: а)  = 0,  = 0.5; б)  = 0.5,  = 1; в)  = 0.4,  = 0.8;

3. Найдите моду и медиану соответствующего одномерного закона распределения вероятностей:

а) Рэлея

;

б) линейно-экспоненциального

;

в) нормального

.

4. На пороговую схему (электронное реле) воздействует случайное напряжение, распределённое по рэлеевскому закону

.

Какова вероятность срабатывания схемы в некоторый фиксированный момент времени , если пороговое значение  В,  = 1 В.

5. Интегральная функция рэлеевского распределения описывается выражением

.

Определите, начиная с какого значения ,  0.997.

6. На входе пороговой схемы, рассмотренной в задаче 4, действует случайное напряжение, имеющее нормальный закон распределения вероятностей с параметрами: 5 мВ,  = 0.5 мВ. Пороговое напряжение схемы  мВ.

Какова вероятность срабатывания схемы в некоторый фиксированный момент времени?

7. Определите и графически изобразите одномерную плотность вероятности w(x) гармонического колебания со случайной начальной фазой, реализация которого имеет вид (рис. 4.3.)

,

где  и  – известные и постоянные для всех реализаций амплитуда и частота;  – начальная фаза, случайная величина для различных реализаций, равномерно распределённая на интервале от 0 до 2p, т. е.  = 1/2p. Круговая частота , где  и – частота и период колебаний.

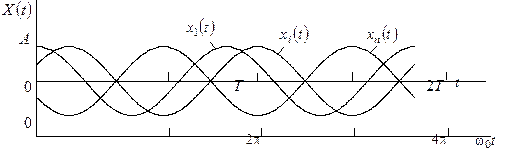
Рис. 4.3

8. По условию предыдущей задачи найдите интегральный закон распределения вероятностей  и определите вероятность того, что  будет находиться в интервале . Проделайте расчёт для случая, когда  и .

9. По графически заданной функции распределения  стационарного случайного процесса (рис. 4.4) определите плотность вероятности  и изобразите примерный вид реализации процесса .

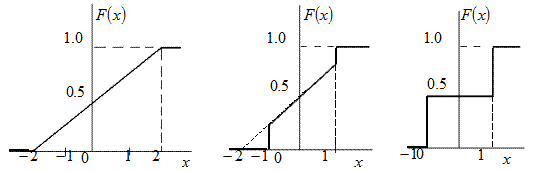
Рис. 4.4

10. Определите и графически изобразите одномерную плотность вероятности пилообразного, треугольного и прямоугольного колебаний (рис. 4.5) с амплитудой , периодом повторения и случайной задержкой , равномерно распределённой на интервале от 0 до Т. Для прямоугольных импульсов скважность принять равной: а) 2; б) 4.

11. Напряжение на выходе пороговой схемы представляет собой случайный процесс , каждая реализация которого  (рис. 4.6) является последовательностью прямоугольных импульсов одинаковой амплитуды А и случайной длительности . Известно, что .

Найдите и изобразите функцию распределения и плотность вероятности этого случайного процесса.

Рис. 4.5

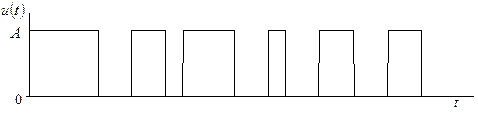
Рис. 4.6

12. Напряжение на выходе измерительного усилителя представляет собой нормальный стационарный случайный процесс с параметрами:  = 0,  = 2 В.

Определите вероятность того, что мгновенное значение напряжения: а) находится в пределах от 0 до 2 В; б) превышает 2 В.

13. По заданному двумерному закону распределения вероятностей

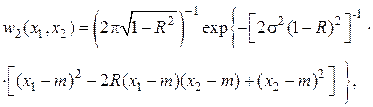
статистически связывающему мгновенные значения  и  нормального стационарного случайного процесса  в сечениях  и , в котором ,  и  – параметры распределения, найдите двумерный закон в независимых сечениях и одномерный закон в сечении .

Найдите также вероятность , т. е. вероятность превышения случайной величиной  порогового уровня .

14. Определите плотность вероятности  случайной величины Z, каждая реализация которой представляет сумму независимых случайных величин  и с заданными законами распределения:

а) экспоненциальным

б) равномерным

в) нормальным с параметрами: , , , .