Качество и эффективность метрологического обеспечения, страница 22

В результате измерений получают значение физической величины, которое отличается от истинного на величину погрешности измерения. Различают абсолютную и относительную погрешности измерения. Абсолютная погрешность измерения определяется соотношением:

                                                      (1)

где X - значение, полученное при измерении; А - истинное значение измеряемой величины.

Относительная погрешность измерения

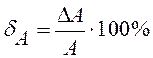                                                       (2)                     

Из соотношений (I) и (2) следует, что для суждения об истинном значении измеряемой величины необходимо не только получить результат измерений, но еще иметь сведения о величине погрешности измерения. По закономерности проявления погрешности могут быть систематическими или случайными. Под систематическими погрешностями понимают погрешности, остающиеся постоянным или закономерно изменяющиеся при повторных измерениях одной и той же величины. Примером систематической погрешности является погрешность градуировки прибора.

Случайными погрешностями называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Они происходят от влияния на результат измерения величин случайного характера, например, погрешность от трения в опорах измерительных приборов. Характерной чертой случайных погрешностей, как и случайных величин, вообще, является то, что их закономерности проявляются лишь при многократном повторении испытаний. Для математического описания случайных величин обычно пользуются методами теории вероятностей и математической статистики. В их основе лежит понятие вероятности появления случайного события. Вероятность есть числовая характеристика степени возможности появлений какого-либо определенною события В  в определенных условиях, которое может повторяться неопределенное число раз. Пусть некоторое испытание повторяется n раз, и во время испытаний событие B появилось m раз. Тогда вероятность появления случайного события B:

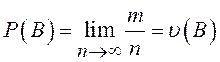                                                                     (3)

где - частота появления события В. Из выражения (3) следует, что 0≤ Р(В)≤1.

Вторым важным понятием теории вероятности является понятие случайной величины. Если результат случайного опыта или эксперимента дается одним скалярным числом X , то величина ξ= X, изображающая соответствующую случайную точку на числовой прямой, зазывается случайной величиной. Типичным примером случайной величины является случайная погрешность измерения. Для количественной характеристики непрерывных случайных величин обычно пользуются плотностью вероятности ω(Х), которая представляет собой  предел отношения вероятности попадания значений случайной величины в малый интервал (X, X + ΔХ) к длине этого интервала ΔХ при Х→0

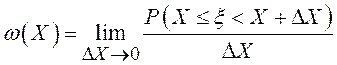
Плотность вероятности ω(Х) обладает следующими: свойствами:

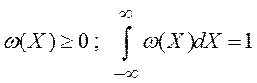                                                              (4)

Вероятность попадания случайной величины в полузамкнутый интервал (a,b) равна интегралу от плотности вероятности в этих пределах:

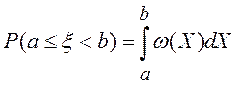                                                                (5)

Иногда вместо плотности вероятности случайной величины ξ пользуются интегральной функцией распределения F₁(X), значение которой в точке X равно вероятности того, что случайная величина ξ примет значение меньшее, чем X:

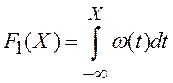                                                                      (6)

Из выражений (4) - (6) следует, что F₁(-∞) = 0;

F₁(+∞) = 1;   P(a ≤ ξ ≤ b) = F₁(b) - F₁(a)

Другими важными числовыми характеристиками случайных величин являются их среднее значение и дисперсия.

Среднее значение (математическое ожидание) m₁ представляет собой неслучайную величину и определяется по формуле:

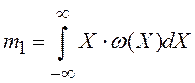
Дисперсия характеризует разброс значений случайной величины относительно среднего значения и определяется по формуле:

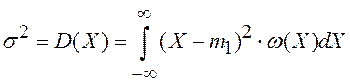
Часто вместо дисперсии пользуются среднеквадратическим отклонением (СКО)

Одним из наиболее распространенных законов распределения результатов измерений является нормальный или гауссовский закон, при котором плотность вероятности задается выражением