Изучение численного метода интерполяции кубическими сплайнами с различными видами граничных условий, страница 3

          Подставляя  в уравнение и используя значения  и , получим следующие уравнения, в которые входят  и соотсоответственно:

 и

          Эти два уравнения можно легко решить относительно  и  и затем их значения подставить в уравнение. В результате получим следующее выражение для кубической функции :

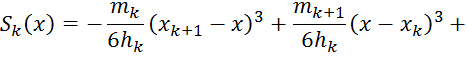
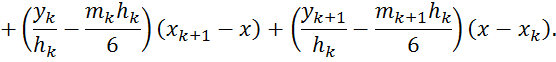
          Заметим, что представление приводится к форме, которая включает только неизвестные коэффициенты {}. Для того чтобы найти их значения, нужно использовать производную от функции, которая имеет вид

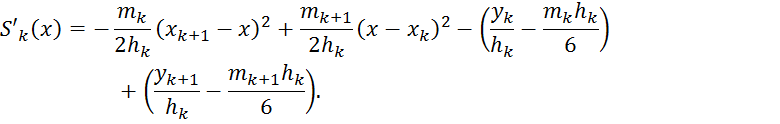
  Вычислив  в точке   и упростив результат, получим:

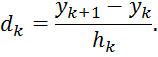
           Подобным образом можно заменить  k на k-1, чтобы получить выражение для , и, вычислив его в точке , получить    

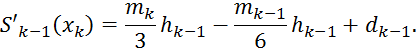
          Учитывая, что вторая производная полученная в результате функции также непрерывна, получим важное соотношение, включающее ,  и

где  k=1,2,…,N-1 [4].

2.3 Построение кубического сплайна

          Система (2.1) является неопределенной системой с N-1 линейным уравнением, включающим N+1 неизвестное, и следует восполнить ее двумя дополнительными уравнениями. Их используют, чтобы исключить   из первого уравнения и  из (N —1)-го уравнения системы. Обычная стратегия для ограничений в крайних точках приведена в таблице 2.1

Таблица  2.1 −  Ограничения в крайних точках для кубического сплайна

          Не обращая внимания на стратегию выбора в таблице 2.1, можно переписать уравнения 1 и N -1 в системе (2.1) и получить трехдиагональную линейную систему формы НМ =V, которая включает  :

          Линейная система (2.2) является строго диагонально доминирующей и имеет единственное решение. После коэффициентов {} коэффициенты {} сплайна  вычисляют по формулам:

          Уравнения (2.1) совместно со стратегией из таблицы 2.1 можно использовать для построения кубического сплайна со свойствами, различными в крайних точках. Точнее говоря, значения и  из таблицы 2.1 используются, чтобы доопределить первое и последнее уравнения системы (2.1) и форму системы из N -1, уравнения заданную в (2.2). Затем трехдиагональная система решается для оставшихся коэффициентов . И наконец, формулы (2.3) используются для вычисления коэффициентов сплайна [3].

2.4 Ограничения в крайних точках

В следующих пяти леммах показана форма трехдиагональной линейной системы, которую следует решать для каждого ограничения в крайних точках из таблицы 2.1.

Лемма 1.1.  Смыкающий сплайн. Существует единственный кубический сплайн, который имеет первую производную с граничными условиями  и

Доказательство. Решим линейную систему

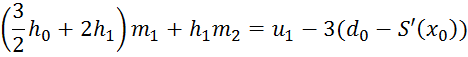
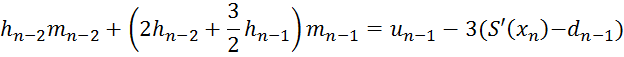
Замечание. Смыкающий сплайн имеет определенный наклон в крайних точках. Этот сплайн можно представить себе как кривую, полученную, когда гибкий эластичный стержень вынужден проходить через заданные точки, и примыкающую к каждому краю с фиксированным наклоном. Этот сплайн может пригодиться чертежнику для того, чтобы рисовать гладкую кривую, проходящую через несколько точек.

Лемма 1.2. Естественный сплайн. Существует единственный кубический сплайн со свободными граничными условиями и .

Доказательство. Решим линейную систему

.

Замечание. Естественный сплайн —это кривая, которую получили, вынуждая гибкий эластичный стержень пройти через заданные точки, но допуская свободный наклон на краях, чтобы обеспечить положение, которое минимизирует осцилляцию кривой. Это полезно для вычерчивания кривой по экспериментальным данным, которые имеют несколько значащих цифр.