Изучение численного метода интерполяции кубическими сплайнами с различными видами граничных условий, страница 9

Во всех случаях при нажатии кнопки для построения кубического сплайна появятся два окна с выводом результата.
          1.  Окно с выводом матрицы коэффициентов сплайна, в соответствии граничных условий (в случае решения, с помощью встроенной функции – вывод значения функции, а в случае построения графиков сплайнов с разными граничными условиями – значений аргументов).
          2.  Окно с выводом графика соответствующего сплайна. 

Вывод результата для смыкающегося сплайна (рис. 5.4.), (рис. 5.5):

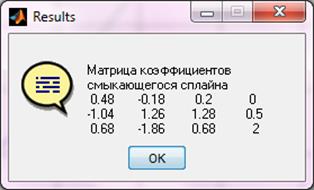
Рисунок 5.4 –Вывод результата для смыкающегося сплайна

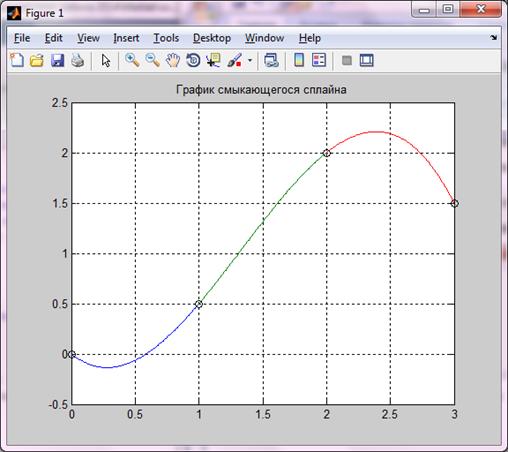
Рисунок 5.5 – График смыкающегося сплайна

Вывод результата для естественного сплайна (рис. 5.6.), (рис. 5.7)

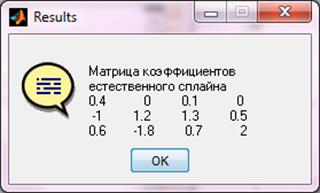
Рисунок 5.6 – Вывод результата для естественного сплайна

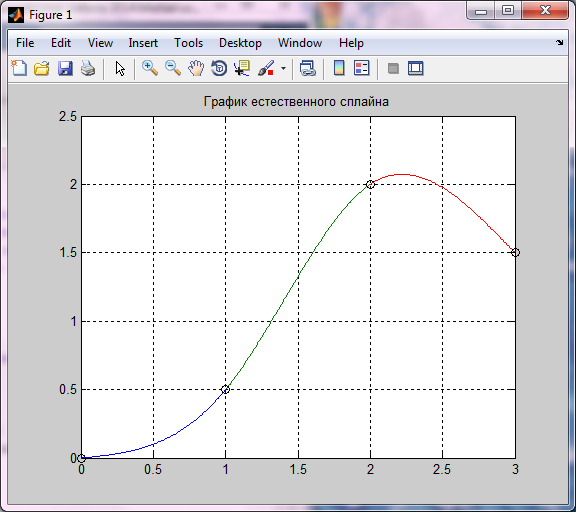
Рисунок 5.7 – График естественного сплайна

Вывод результата для экстраполяционного сплайна (рис. 5.8.),
(рис. 5.9)

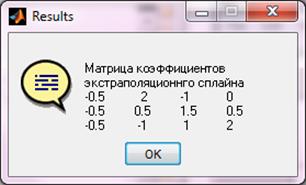
Рисунок 5.8 – Вывод результата для смыкающегося сплайна.

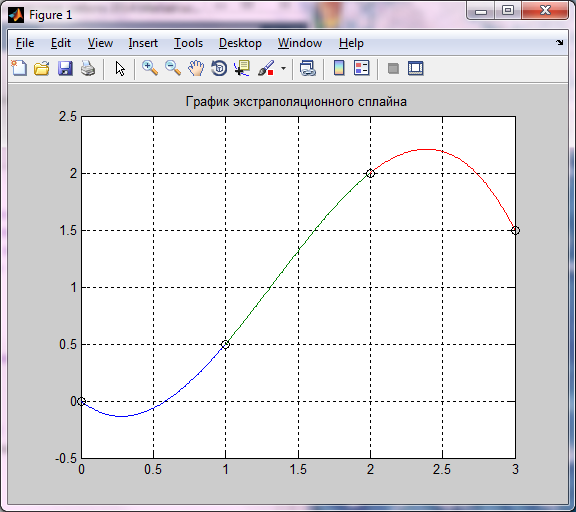
Рисунок 5.9 – График экстраполяционного сплайна

Вывод результата для сплайна  заканчивающегося параболой (рис. 5.10.), (рис. 5.11)

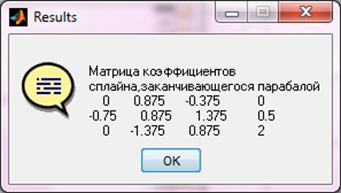
Рисунок  5.10 – Вывод результата для сплайна заканчивающегося параболой

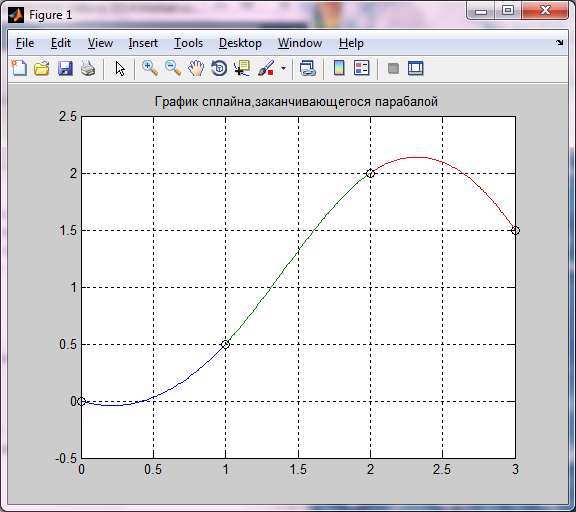
Рисунок  5.11 – График сплайна заканчивающегося параболой

Вывод результата для сплайна  с заданной кривизной (рис. 5.12), (рис. 5.13)

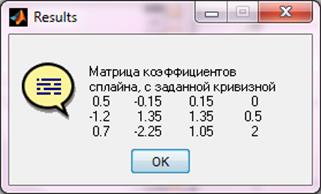
Рисунок 5.12 - Вывод результата для сплайна  с заданной кривизной

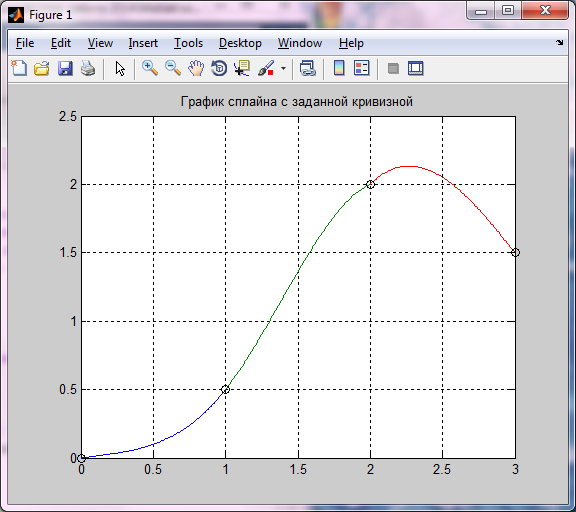
Рисунок 5.13 - График сплайна  с заданной кривизной

Построение сплайна, с помощью встроенных функций
(рис. 5.14.), (рис. 5.15).

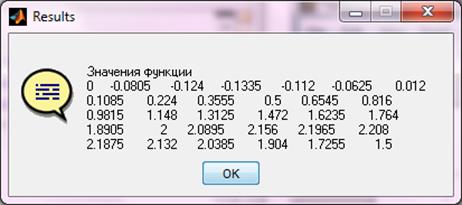
Рисунок 5.14 –Вывод значений функции, подсчитанных, с помощью встроенной функции

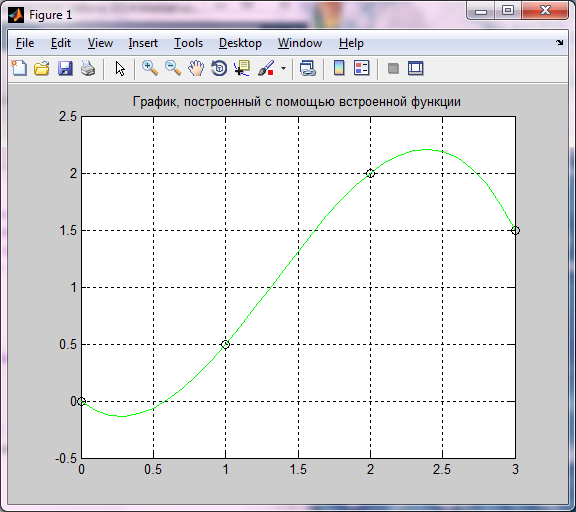
Рисунок 5.14 –График сплайна построенного, с помощью встроенных функций

Вывод графиков кубических сплайнов с разными граничными условиями (рис. 5.16.), (рис. 5.17).

Рисунок 5.16 – Значения аргумента в заданных точках.

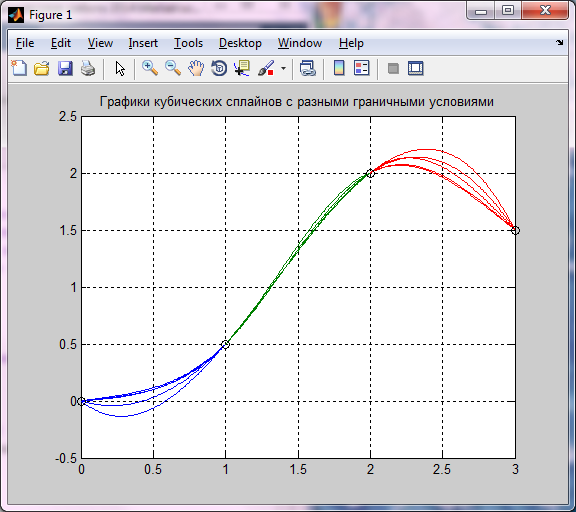
Рисунок 5.14 –Графики кубических сплайнов, с разными граничными условиями

ВЫВОДЫ

В данной курсовой работе изучено  интерполирование кубическими сплайнами с различными граничными условиями. В прикладном пакете Matlab  реализовано программное обеспечение  для  построения кубических сплайнов. Программа работает для общего случая и позволяет пользователю, в зависимости от исходных данных, выбирать граничные условия. Проведено тестирование на функции заданной 4 точками и известными значениями первой и второй производной на концах интервала. Построенные графики наглядно демонстрируют влияние граничных условий на вид функции.  Сделаем выводы по каждому граничному условию.

Смыкающий сплайн имеет определенный наклон в крайних точках. Этот сплайн может пригодиться чертежнику для того, чтобы рисовать гладкую кривую, проходящую через несколько точек.

Естественный сплайн полезен для вычерчивания кривой по экспериментальным данным, которые имеют несколько значащих цифр.

Экстраполяционный сплайн эквивалентен предположению, что край кубического полинома является продолжением смежного кубического полинома.

Сплайн, заканчивающийся параболой заставляет кубическую кривую вырождаться в параболу на интервале [; ] и подобная ситуация происходит на интервале [; ].

Сплайн с заданной кривизной. Задавая значения , профессионал имеет возможность получать нужную кривизну в каждой крайней точке.

Если известны значения первых производных в граничных точках, оптимальным выбором будет смыкающий сплайн.

СПИСОК ЛИТЕРАТУРЫ

1.  Интерполяция [Электронный ресурс] — Режим доступа: http://арmath.spdu/ru/ru/staff/tuzov/onapr.html/ — 13.10.2014 г.

2.  Патокина,  А. В. Численные методы с использованием математических пакетов NATLAB и MATHCAD [Текст] / учеб. Пособие по лаб. практикуму / А. В. Потокина, О. В. Яровая. – Х. : Нац. аэрокосм. ун-т «Харьк.авиац. ин-т», 2008. – 82с.

3.  Метьюз, Джон,  Г.  Численные методы.  Использование MatLab [Текст] / Джон Г. Метьюз, Куртис Д. Финк.  ––  М.: Изд. дом «Вильямс»,  2001. –– 713 с.

4.  Демидович, Б. П. Основы вычислительной математики [Текст] / Б.П. Демидович, И.А. Марон .–– М.: Наука, 1966. ––  663 c.