Кубические сплайны лишены этого недостатка. Исследования теории балок показали, что гибкая тонкая балка между двумя узлами достаточно хорошо описывается кубическим полиномом, и поскольку она не разрушается, то аппроксимирующая функция должна быть, по меньшей мере, непрерывно дифференцируемой. Это означает, что функции ϕ(x), ϕ'(x), должны быть непрерывными на отрезке [a, b] [1].
Полезное
свойство, которым обладают сплайны — это минимизация колебательного поведения. Следовательно,
среди всех дважды дифференцируемых, непрерывных на интервале [a;b]
функций f(x),
интерполирующих заданную совокупность точек ![]() кубический сплайн меньше всего
осциллирует. Следующий результат объясняет этот феномен.
кубический сплайн меньше всего
осциллирует. Следующий результат объясняет этот феномен.
Миминизирующее свойство кубического сплайна. Если, ![]()
![]() —единственный кубический сплайн,
которым интерполируют функцию
—единственный кубический сплайн,
которым интерполируют функцию ![]() (x), проходящий через точки
(x), проходящий через точки ![]() и удовлетворяющий условиям
смыкания на краях
и удовлетворяющий условиям
смыкания на краях ![]() ,
, ![]() . Тогда
. Тогда
![]() .
.
Пусть на отрезке [a, b] имеется
таблично заданная функция
а = ![]() <
< ![]() <…<
<…< ![]() = b. Шаг таблицы может быть непостоянным. Постановка
задачи: На отрезке [a, b] необходимо найти функцию g(x), которая
удовлетворяет следующим требованиям:
= b. Шаг таблицы может быть непостоянным. Постановка
задачи: На отрезке [a, b] необходимо найти функцию g(x), которая
удовлетворяет следующим требованиям:
1. Сплайн g(x) ![]() (a,b),
т.е. g(x), g'(x), g''(x) непрерывны на отрезке [a,b], график g(x)
не имеет острых углов (т.к. g'(x)
непрерывна), радиус кривизны определен в каждой точке.
(a,b),
т.е. g(x), g'(x), g''(x) непрерывны на отрезке [a,b], график g(x)
не имеет острых углов (т.к. g'(x)
непрерывна), радиус кривизны определен в каждой точке.
2. На каждом участке g(x) является
кубическим полиномом III степени, т.е. 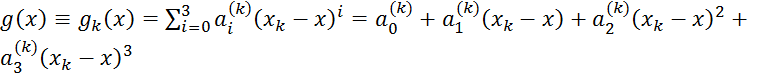 , где
, где ![]() – коэффициенты сплайна, которые
определимы из дополнительных условий: k=( 1… n) – номер сплайна.
– коэффициенты сплайна, которые
определимы из дополнительных условий: k=( 1… n) – номер сплайна.
3.
Выполняется основное условие интерполяции: ![]()
![]() .
.
4.
Вторая производная g''(x)
удовлетворяет граничным условиям. В общем случае эти условия зависят от
конкретной задачи. Довольно часто используется условие свободных концов
сплайнов, а именно
g''(a)
= g''(b)
= 0.
В результате построения с соблюдением всех условий будем иметь:
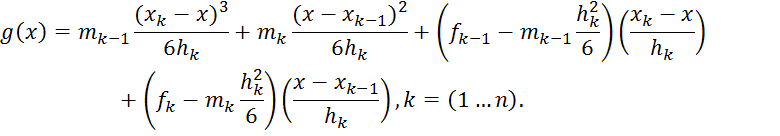
Для
определения неизвестных ![]() используем непрерывность g'(x).
В результате получим систему для определения
используем непрерывность g'(x).
В результате получим систему для определения ![]() с n-1
уравнением и n+1
неизвестными. Её нужно доопределить для однозначного решения. Дополняем
систему граничными условиями, например условиями свободных концов сплайна
с n-1
уравнением и n+1
неизвестными. Её нужно доопределить для однозначного решения. Дополняем
систему граничными условиями, например условиями свободных концов сплайна ![]() .
Получаем систему n-1
уравнения с n-1
неизвестными:
.
Получаем систему n-1
уравнения с n-1
неизвестными:
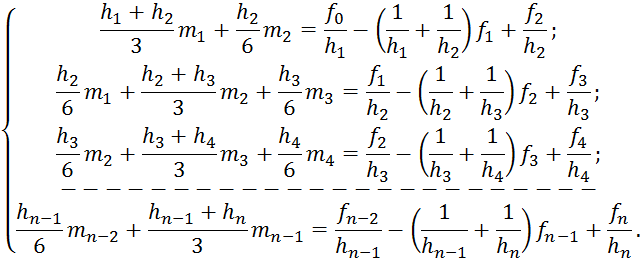
В
матричном виде систему можно записать следующим образом: A![]() =F
=F![]() , где
, где
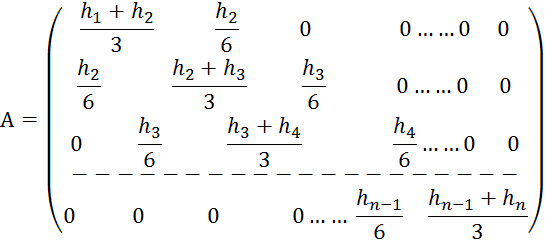
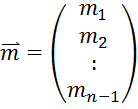
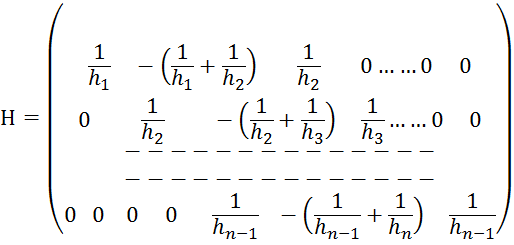
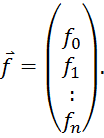
Матрица А – неособенная матрица, система для определения m имеет единственное решение, следовательно, сплайн-функция g(x) однозначно восстанавливается, т.е. задача о нахождении кусочно-кубической функции g(x) имеет единственное решение. Решение системы может быть найдено с помощью метода прогонки (частный случай метода Гаусса) или каким-либо другим способом [2].
Каждый
кубический полином ![]() (x) имеет 4 неизвестные постоянные
(
(x) имеет 4 неизвестные постоянные
(![]() ), поэтому существует 4N коэффициентов,
которые нужно найти. Неточно говоря, есть 4N
степеней свободы или условий, которые должны быть точно определены. Заданные
точки обеспечивают N + 1 условие, и каждое из свойств III—V обеспечивает
N —1 условие. Следовательно, задаются N + 1 + 3(N —1) = 4N —2
условия. Это оставляет две степени свободы. Будем называть их ограничениями в
крайних точках: они будут включать либо S′(x), либо S′′(x) в
точках
), поэтому существует 4N коэффициентов,
которые нужно найти. Неточно говоря, есть 4N
степеней свободы или условий, которые должны быть точно определены. Заданные
точки обеспечивают N + 1 условие, и каждое из свойств III—V обеспечивает
N —1 условие. Следовательно, задаются N + 1 + 3(N —1) = 4N —2
условия. Это оставляет две степени свободы. Будем называть их ограничениями в
крайних точках: они будут включать либо S′(x), либо S′′(x) в
точках ![]() и
и ![]() . А сейчас продолжим построение.
. А сейчас продолжим построение.
Так
как S(x) —кусочно-кубический полином, его вторая производная S"(х)
кусочно-линейна на интервале [![]() ,
, ![]() .]. Формула линейного
интерполирования Лагранжа дает следующее представление для
.]. Формула линейного
интерполирования Лагранжа дает следующее представление для
![]() :
:
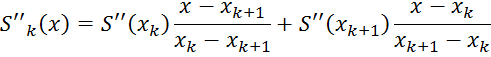
![]() ,
, ![]()
![]()
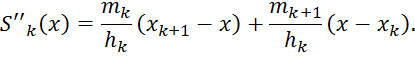
Для ![]() и k=0,
1,…,N-1.
Интегрируя уравнение дважды, введем две постоянные интегрирования. Результат
можно преобразовать так, что он примет вид
и k=0,
1,…,N-1.
Интегрируя уравнение дважды, введем две постоянные интегрирования. Результат
можно преобразовать так, что он примет вид
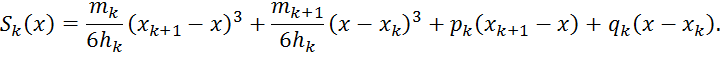
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.