Алгоритм создания машин и механизмов. Пространство, в котором существуют механизмы. Основные виды механизмов. Аналитические методы исследования кинематики машин, страница 9

-  Записываем векторное уравнение скорости точки С

    (1)

-  Анализируем векторное уравнение

                 (2)

V_C - ?       V_C  // X

-  Строим на плане скоростей уравнение 1

-  Находим истинное значение скорости

       (по правилу обозначение отрезка пишется от вершины вектора)

-  Из уровня (2) находим, что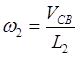

-  Найдем скорость точки F

               (3)

         (4)

-  Строим план скоростей точки F

Свойства плана скоростей (рис. 1. а).

1.  Все скорости выходящие из полюса являются абсолютными скоростями исследования.

2.  Вектора, не проходящие через Р_r ,  являются относительно скоростными точками.

3.  Скорости точек, лежащие в полюсе плана скоростей равны 0.

4.  Т. подобия. Фигура, образованная в результате жесткого соединительного соединения концов векторов абсолютных скоростей подобна и повернута на 90⁰ фигуре на плане положений.

(Скорость точки F находится из подобия ).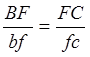

Построение плана ускорений (рис. 1. б).

1.  Построить планы скоростей.

2.  Находим ускорение точки В.

         (1)

                                                          

                   к центру вращения.

3.  Выбираем полюс ускорений (π).

4.  Откладываем b произвольной длины вектор .

5.  Находим          в сторону ε₁.

6.  Определяем масштабный коэффициент ускорения.

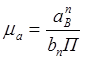
7.  Находим отрезок, который будет изображать тангенциальное ускорение на плане ускорений.

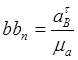
8.  Строим на плане ускорений bb_n.

9.  Соединив П и b, мы находим абсолютное ускорение точки В.

10.  Определим истинное ускорение точки В.

11.  Находим ускорение точки С.

           (2)

                                            

 к точке В

12.  Находим отрезок, который будет изображать на плане ускорений .

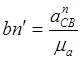
13.  Откладываем bn' на плане ускорений.

14.                                                (3)

15.  Из точки bn' проводим след  .

16.  Проводим след ускорения точки С через полюс П.

17.  Находим истинное значение

 - вектор Сb

18.  Находим угловое ускорение второго звена из (3)

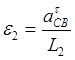
19.  Находим напр. углового ускор. зв. 2., для чего вектор условно переносим в точку С.

Свойства планов ускорений.

Полностью аналогичны свойствам планов скоростей. Единственное отличие состоит в том, что жесткая фигура на плане ускорений поворачивается на угол, отличный от 90⁰.

Особенности кинематического анализа кулисных механизмов.

Кулисным называется механизм,  у которого имеется подвижная направляющая.

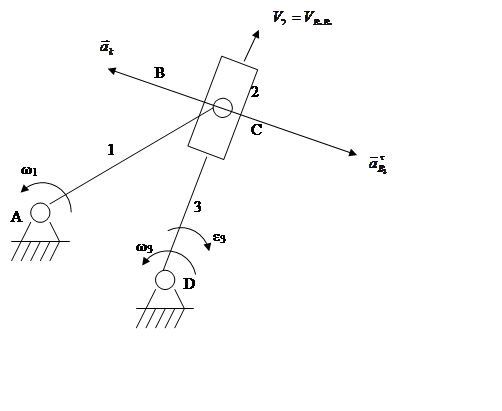
1 – кривошип

2 – камень

3 – кулиса

Особенностью кулисных механизмов является то, что В принадлежит 3-м звеньям.

 кривошипу

 камню

 кулисе

Звено 2 совершает сложное движение, т. е. у него естьV- относительная и  ω – переносная, таким образом, появляется дополнительное ускорение а_к.

      - для плоских механизмов

Правило определения направления кариолиса.

1.  Определим направление V_отн и ω_пер

2.  Если смотреть на вектор переносной скорости (ω₃), тогда поворачиваем вектор относительной скорости (V₂) угол 90⁰ в сторону вращения ω₃  получим .

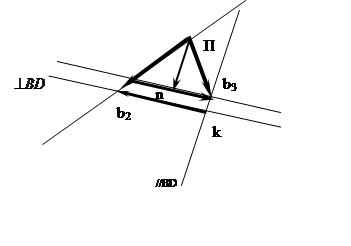
Постороение планов скоростей кулисного механизма.

1.  Проводим структурный анализ.

2.  Строим планы положения.

3.  Строим планы скоростей.

3.1.  Определяем скорость точки В₁.

        

3.2.  Выбираем полюс плана скоростей.

3.3.  Из точки p_V откл. произвольной длины вектор скорости .

3.4.  Определяем масштабный коэффициент

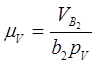
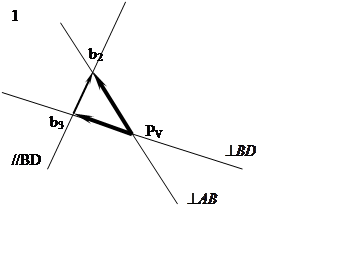
3.5.  Определив скорость точки В₃

  (1),

решим (1) относительно

                                                                       (2)

                                                                   

анализируем (2).

3.6.  Строим векторное ускорение (2) на плане скоростей.

3.7.  Находим истинное значение скоростей.

3.8.  Находим ω₃.

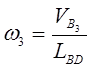
3.9.  Находим направление угловой скорости ω₃.

4.  Строим планы скоростей для других положений.