В данном случае неравенство ![]() в контрольной
точке не выполняется. Значит, оно выполняется в противоположной плоскости на
рис.4.1 (заштрихована).
в контрольной
точке не выполняется. Значит, оно выполняется в противоположной плоскости на
рис.4.1 (заштрихована).
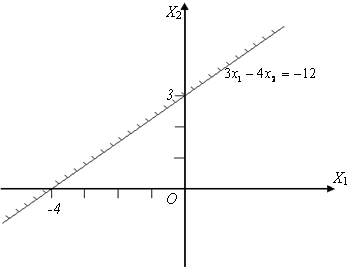 |
Рис. 4.1
2. ![]() .
.
Прямая проходит через начало координат. За вторую точку можно взять любую, лежащую на прямой, например А (2;3)
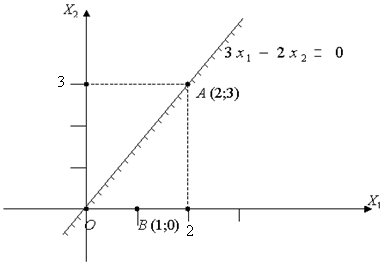 |
Рис. 4.2
В качестве контрольной точки возьмём любую не лежащую на прямой, Например В(1;0).
В этой точке 3–2∙0 > 0 неравенство выполняется. Значит область решений неравенства – нижняя полуплоскость (заштрихована, рис.4.2).
Множество точек, удовлетворяющих уравнению ![]() при
при
![]() является плоскостью, при
является плоскостью, при ![]() – гиперплоскостью. В этом случае
теорему о решении неравенства, содержащего n неизвестных можно обобщить
следующим образом.
– гиперплоскостью. В этом случае
теорему о решении неравенства, содержащего n неизвестных можно обобщить
следующим образом.
Теорема.
Область решения неравенства с n переменными ![]() есть одно из полупространств, на
которые все пространство делится гиперплоскостью
есть одно из полупространств, на
которые все пространство делится гиперплоскостью ![]() ,
включая и эту гиперплоскость.
,
включая и эту гиперплоскость.
4.2. Множество решений системы неравенств.
Множеством решений системы линейных неравенств являются точки, которые принадлежат полуплоскостям решений всех неравенств, т.е. принадлежат их пересечению.
Рассмотрим конкретный пример.
Пример 4.2.
Построить
множество решений системы неравенств.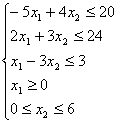
Для определения множества решений системы неравенств строим последовательно множество решений каждого неравенства.
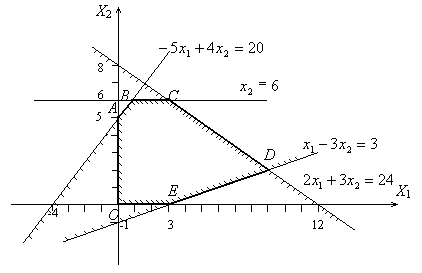 |
Рис.4.3
В рассматриваемом примере областью решений системы неравенств является так называемый выпуклый многоугольник.
Выпуклой фигурой называется фигура, обладающая следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. Координаты угловых точек – вершин этого многоугольника найдём как координаты точек пересечения соответствующих прямых.
Например, координаты точки D найдём, решая совместно систему уравнений

При построении области решений системы неравенств могут встретится и другие случаи:
- многоугольная область (рис.4.4.)
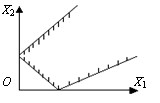
Рис. 4.4
- одна точка (рис.4.5)
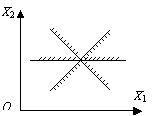 |
Рис.4.5
- пустое множество, когда система неравенств несовместна (рис. 4.6)
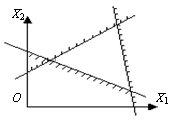
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.