Теория электромагнитного поля. Закон Кулона. Теорема Гаусса в интегральной форме, страница 4

Разделим её на столь малые части, что поверхность каждой из них можно считать практически плоской. Проведём к каждому элементу поверхности вектор   по направлению к наружной поверхности, причём длина в выбранном масштабе равна площади данного элемента.

Обозначим  - вектор электрической индукции на элементе поверхности j. Назовём скалярное произведение -потоком вектора через элемент поверхности j.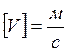  

           

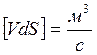
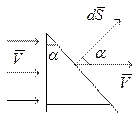
Рассмотрим движение жидкости, которую можно отобразить полем  (линейная скорость жидкости), тогда скалярное произведение  есть поток воды через элемент поверхности .

Складывая потенциал через все элементы поверхности, получим поток вектора  через всю поверхность:

, где -поток вектора через всю поверхность.

Уменьшая площадь элементов, переходим к интегралу по поверхности:

.

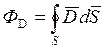Предположим, что поверхностью является сфера, а поле создаётся точечным зарядом, расположенным в центре сферы.

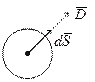
Тогда поток вектора :

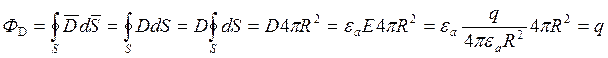
Таким образом, из полученного выражения следует, что поток вектора электрической индукции не зависит от размеров сферы и равна заряду внутри неё.

Математически установлено, что поток через любую замкнутую поверхность охватывающею заряд  равен потоку через сферу, то есть самому заряду.

Пусть имеем  зарядов создающих поле, составляющие индукции которого .

Тогда результирующий поток определяется:

, ,…

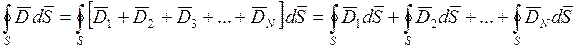
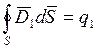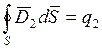Первая форма записи теоремы Гаусса в интегральной форме.

Поток вектора электрической индукции через любую замкнутую поверхность, окружающую некоторый объём, равен алгебраической сумме свободных зарядов, находящихся в этом объёме.

Свободные заряды – заряды, которые под воздействием сил поля перемещаются в среде, причём их перемещения не ограничиваются внутри молекулярными силами (пример: ионы газа).

Смысл введения вектора электрической индукции состоит в том, что его поток через любую замкнутую поверхность определяется только свободными зарядами, не всеми зарядами внутри объёма. Это позволяет не рассматривать связанные заряды, что приводит к упрощению решения многих задач.         

Вторая форма записи Теоремы Гаусса.

В однородном и изотропном диэлектрике:

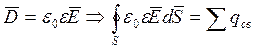, тогда ,

Из последнего выражения следует, что напряжённость, это такая характеристика поля, которая зависит от диэлектрических свойств среды.

Третья форма записи Теоремы Гаусса.

Поток вектора напряжённости через любую замкнутую поверхность, не только суммой свободных зарядов, но и суммой связанных зарядов, находятся внутри этой поверхности.

Теорему Гаусса в интегральной форме используется для определения напряжённости  или индукции  в какой-либо точке поля, если через эту точку можно провести замкнутую поверхность так, чтобы все точки этой поверхности оказались в одинаковых (симметричных) условиях относительно заряда созданного поя.

                

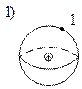
Такой поверхностью является сфера (если заряд точечный) или поверхность цилиндра (если заряд линейный).

Однако по величине интеграла (в левой части) Теоремы Гаусса нельзя судить о распределение элементарного заряда внутри объёма ограниченной замкнутой поверхности.

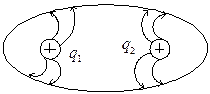
Для решения этого вопроса необходимо воспользоваться Теоремой Гаусса в дифференциальной форме.

Теорема Гаусса в дифференциальной форме.

Позволяет выяснить, находится ли элементарный заряд в малом объёме  , заключающем в себе точку А и какова объёмная плотность заряда в этой точке.

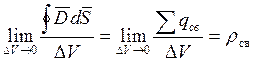-(объёмная плотность свободных зарядов).

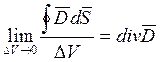
Левая часть полученного выражения есть величина конечная и называется дивергенцией расхождения вектора

-первая форма записи теоремы Гаусса в дифференциальной форме.

В декартовой системе координат расписывается по формуле:

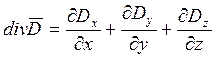
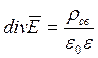-вторая форма записи теоремы Гаусса в дифференциальной форме.

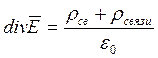
Если в данной точке поля , то через поверхность, ограничивающую, эту поверхность расходятся в окружающем её пространстве (положительный заряд – «источник» линий напряжённости); если , то сходятся из окружающего его пространства (отрицательный заряд-«сток» линий напряжённости). Поле в области, где дивергенция равна нулю, называется солиноидальным (трубкообразным).

Выше было показано, что умножение вектора набла на скалярную величину даёт градиент этой скалярной величины . Умножение набла на векторную величину даёт дивергенцию этой векторной величины.