Если известен закон изменения потенциала в любой точке
поля, то можно определить и напряжённость в любой точке. Действительно в декартовой
системе координат вектор ![]() можно представить в
виде:
можно представить в
виде:
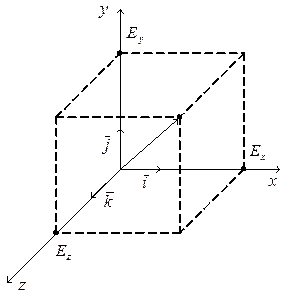
![]()
учтём, что
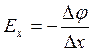 ;
; 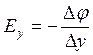 ;
; 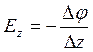 .
.
Тогда
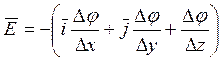
Уменьшая приращения по осям и переходя к пределу, получим:
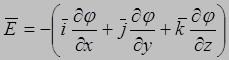 (9)
(9)
(9) связь между зарядом и полем в дифференциальной форме.
Выражение
в скобках градиент скалярной величины ![]() .
.
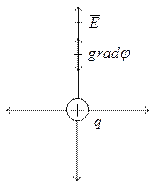
Градиент-вектор направление наискорейшего изменения некоторой величины, значение которой изменится от одной точки пространства к другой.
![]() (-)
(-)
Закон (-) говорит то, что напряжённость и градиент направлены в противоположные стороны.
Существует ещё одна форма записи градиента через
дифференциальный оператор Гамильтона. Набла ![]() -сумма
частных производных по отдельным координатным осям умноженным на
соответствующие одиночные векторы.
-сумма
частных производных по отдельным координатным осям умноженным на
соответствующие одиночные векторы.
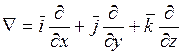
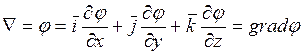
![]()
При графическом изображении полей, кроме силовых линий так же строят эквипотенциальные поверхности (поверхности равного потенциала). След пересечения эквипотенциальной поверхности с плоскостью чертежа, называют эквипотенциальной линией.
Уравнение эквипотенциальной
поверхности или линии, ![]() .
.
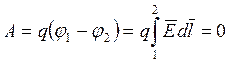
Поскольку при перемещение заряда вдоль эквипотенциали
работа не совершается, то ![]() силовые и
эквипотенциальные линии пересекаются под углом 90 градусов.
силовые и
эквипотенциальные линии пересекаются под углом 90 градусов.
Обычно при построении картины поля эквипотециали
проводят так что бы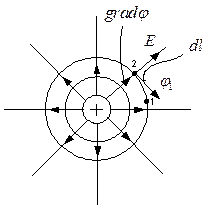 между соседними (смежными)
всегда была одна и та же разность потенциалов, тогда густота эквипотенциальных
линий даёт возможность судить о напряжённости поля (там где они расположены
ближе друг к другу, напряжённость поля больше).
между соседними (смежными)
всегда была одна и та же разность потенциалов, тогда густота эквипотенциальных
линий даёт возможность судить о напряжённости поля (там где они расположены
ближе друг к другу, напряжённость поля больше).
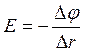
Диэлектрики в электростатическом поле. Вектор поляризации.
Различают диэлектрики: с полярными и неполярными молекулами.
У неполярных диэлектриков (H, N, слюда, парафин) при отсутствии внешнего поля ядра, атомы находятся в центре орбит электронов, и атомы (молекулы) являются электрически нейтральными.

![]()
При появлении внешнего поля орбиты электронов смещаются в направлении противоположному полю, и ядро атома оказывается смещённым относительно центра электронных орбит:
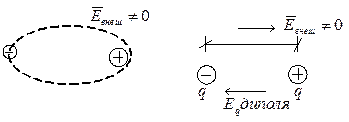
Такой атом можно рассматривать как электрический диполь, то есть как пару разноимённых зарядов, находящихся на расстоянии 4 друг от друга.
Величина (дальность) расхождения зарядов 4, ограниченно внутримолекулярными силами и поэтому такие заряды называются связанными.
При исчезновении внешнего поля исчезает и смещение электронных орбит.
У полярных диэлектриков (хлористый N) молекулы и при отсутствии внешнего поля образуют диполи, расположенные хаотически в объёме диэлектрика.
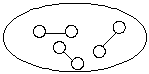
При появлении внешнего поля диполи полярного диэлектрика ориентируются по полю.
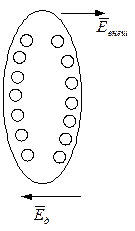
Таким образом в полярных и неполярных диэлектриках при наличии внешнего поля диполи ориентируются по полю.
Явление изменения расположения связанных зарядов в диэлектрике, вызванным внешним полем называется поляризацией.
Электростатическое поле диполей ослабляет внешнее поле
и результирующая напряжённости поля в диэлектрике ![]() . Это
ослабление учитывается с помощью относительной диэлектрической проницаемости
. Это
ослабление учитывается с помощью относительной диэлектрической проницаемости ![]() , которая показывает во сколько раз
результирующая напряжённость в веществе меньше напряжённости в вакууме.
, которая показывает во сколько раз
результирующая напряжённость в веществе меньше напряжённости в вакууме.
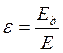
Назовём электрическим моментом диполя вектор ![]() , направленный от “-“ заряда к “+“:
, направленный от “-“ заряда к “+“:
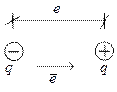
Мерой поляризации вещества является вектор поляризации равный электрическому моменту диполя к единице объёма вещества:
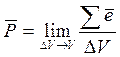
Среда во всех точках которой ![]() для
поле любых направлений называется однородной.
для
поле любых направлений называется однородной.
Среда проявляющая различные свойства, в зависимости от напряжения поля называется анизотропной.
Для большинства изотропных сред вектор поляризации пропорционален напряжённости поля:
![]()
k-электрическая (диэлектрическая) восприимчивость вещества.
Вектор электрической индукции.
Электрическим смещением (электрической индукцией ![]() ) называется векторная величина характеризующая
электростатическое поле.
) называется векторная величина характеризующая
электростатическое поле.
Для вакуума:![]()
Для поля в диэлектрике ![]() (*)
(*)
Кроме
того для изотропного диэлектрика выполняется ![]() (**).
(**).
Сравнивая (*) и (**):
![]()
Теорема Гаусса в интегральной форме.
Начнём с определения величины называемой потоком. Рассмотрим в электростатическом поле произвольную замкнутую поверхность.
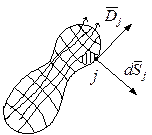
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.