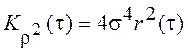Нормальный случайный процесс, страница 5

.

Среднее значение квадрата огибающей равно . Проверить это мы просим читателя.  В качестве упражнения предлагается также найти спектральную плотность квадрата огибающей, если известна спектральная плотность  исходного узкополосного нормального процесса, например, для полосового шума с прямоугольным энергетическим спектром.

Информацию о вероятностных характеристиках фазы узкополосного нормального процесса можно получить с помощью [9].

Функционал плотности вероятности (ФПВ) нормального случайного процесса

Выше неоднократно отмечалось, что любая совокупность п отсчетов нормального случайного процесса описывается многомерным нормальным распределением

,

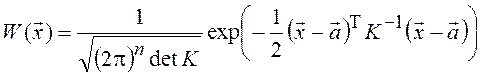где  – вектор отсчетов описываемого нормального случайного процесса (x_i = x(t_i));  – вектор средних значений для рассматриваемых отсчетов;  – корреляционная матрица, элементами которой являются ковариации отсчетов, т. е. .

Если процесс имеет финитный спектр, т. е. S(f) = 0 при | f | > F,то совокупность отсчетов, взятых с интервалом , полностью его определяет (теорема Котельникова). В случае неограниченного спектра (конечный интервал наблюдений [0, T]) требуется осуществить предельный переход в формуле для , устремляя  к нулю, а  к бесконечности. Запишем  в развернутой форме:

,

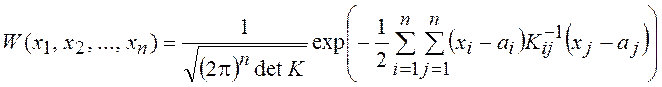где x_i = x(t_i),  – элементы матрицы, обратной K. Учтем, что

,

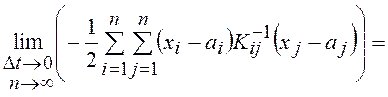
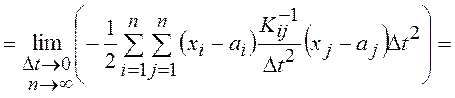
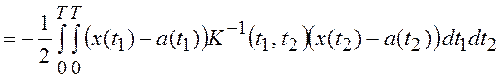где 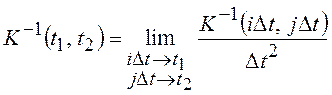 – обратная корреляционная функция, удовлетворяющая интегральному уравнению

,

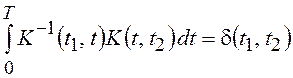которое вытекает из соотношения, связывающего элементы матрицы K и обратной K^–1: 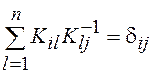, где 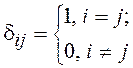 – символ Кронекера, превращающийся в дельта-функцию в результате предельного перехода

,

.

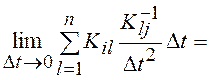
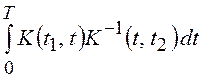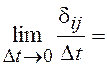
Если процесс x(t) является стационарным и интервал наблюдения велик по сравнению с временем корреляции, то интегральное уравнение для обратной корреляционной функции можно переписать следующим образом:

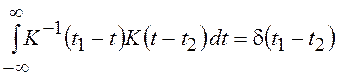
и решить его с помощью теоремы о свертке, применив к обеим частям преобразование Фурье. Для этого выполним замену переменной t – t₂ = xи введем переменную t₁ – t₂ = t. Получим:

,

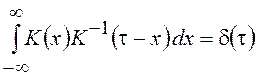откуда следует, что  и , где F – оператор Фурье, S(w) – спектральная плотность процесса x(t).

Обозначая 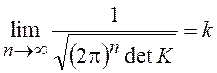, получим окончательно:

,

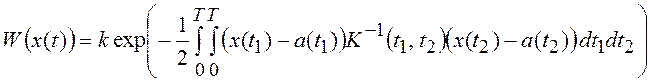где a(t) – среднее значение процесса x(t).

Если x(t) – нормальный “белый” шум с КФ 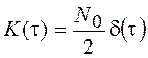, то

,

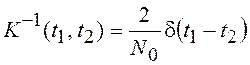и используя интегральное (фильтрующее) свойство дельта-функции получим выражение для функционала плотности вероятности нормального белого шума

.

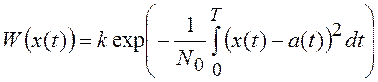Таким образом, вероятность появления реализации нормального белого шума x(t) зависит от ее евклидова расстояния относительно среднего значения a(t).

Контрольные вопросы

1. Дайте определение нормального СП.

2. Стационарный нормальный СП имеет . Запишите одномерную ПВ производной для момента времени .

3. Дайте определение винеровского процесса.

4. Дайте определение узкополосного нормального СП.

5. Как определяется комплексная огибающая СП? Какие свойства имеет огибающая (комплексная огибающая) СП?

6. Запишите квадратурное представление узкополосного СП.

7. Какие статистические характеристики имеют амплитуды квадратурных составляющих  и  для узкополосного нормального СП?

8. Какой будет совместная ПВ огибающей  и фазы  узкополосного СП? Будут ли  и  зависимыми СВ?

9. Как изменится ситуация при добавлении к узкополосному нормальному СП гармонического сигнала , где  - центральная частота энергетического спектра СП.

10. В чем состоит методика определения совместных ПВ огибающей и фазы для отсчетов, разделенных промежутком ?

11. Что такое функционал плотности вероятности нормального СП?

12. Как выглядит ФПВ для нормального «белого» шума?