6. Запишите ПВ случайной
величины 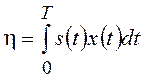 , где
, где ![]() - нормальный
«белый» шум с
- нормальный
«белый» шум с 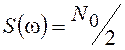 ,
, ![]() -
детерминированная функция.
-
детерминированная функция.
7. На вход интегрирующей RC-цепи с постоянной времени ![]() в момент времени
в момент времени ![]() подается
сумма постоянного сигнала и «белого» шума с
подается
сумма постоянного сигнала и «белого» шума с 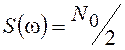 .
Найти среднее значение и дисперсию СП на выходе цепи. Будет ли этот процесс
стационарным?
.
Найти среднее значение и дисперсию СП на выходе цепи. Будет ли этот процесс
стационарным?
8. Как связаны в
установившемся режиме линейной цепи с коэффициентом передачи ![]() СПМ на входе и выходе цепи?
СПМ на входе и выходе цепи?
Глава 7. Нормальный случайный процесс
Следствием центральной
предельной теоремы является чрезвычайно широкое распространение в радиотехнике
и других областях науки и техники нормального случайного процесса. Если
выполняется условие ![]() , где
, где ![]() –
полоса пропускания линейной системы, а
–
полоса пропускания линейной системы, а ![]() –
эффективная ширина спектра входного случайного процесса, то значения выходного
СП в произвольный момент времени можно приближенно рассматривать как взвешенную
сумму
–
эффективная ширина спектра входного случайного процесса, то значения выходного
СП в произвольный момент времени можно приближенно рассматривать как взвешенную
сумму ![]() независимых случайных величин. При этом
независимо от распределения отсчетов входного СП предполагается, что условия
центральной предельной теоремы выполняются. Тогда выходной процесс будет приближенно
нормальным. Очевидно, что степень приближения зависит от числа независимых
слагаемых
независимых случайных величин. При этом
независимо от распределения отсчетов входного СП предполагается, что условия
центральной предельной теоремы выполняются. Тогда выходной процесс будет приближенно
нормальным. Очевидно, что степень приближения зависит от числа независимых
слагаемых ![]() и распределения отсчетов входного процесса.
Это явление называют эффектом нормализации.
и распределения отсчетов входного процесса.
Это явление называют эффектом нормализации.
Совокупность отсчетов
нормального СП образует нормальный случайный вектор ![]() ,
статистические свойства которого были подробно рассмотрены выше. Следствием
этих свойств является то обстоятельство, что нормальный случайный процесс
полностью определяется математическим ожиданием
,
статистические свойства которого были подробно рассмотрены выше. Следствием
этих свойств является то обстоятельство, что нормальный случайный процесс
полностью определяется математическим ожиданием 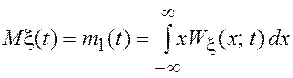 и
корреляционной функцией
и
корреляционной функцией 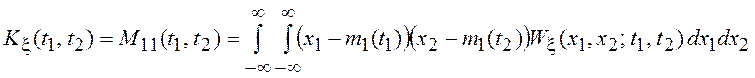 , т. е. его полное
описание дается в рамках корреляционной теории.
, т. е. его полное
описание дается в рамках корреляционной теории.
Если нормальный СП подвергается линейному преобразованию, то в результате мы получаем нормальный случайный процесс, если преобразование осуществляется с помощью оператора, либо нормальную случайную величину, если речь идет о линейном функционале от нормального СП.
Например, производная дифференцируемого
стационарного нормального СП есть стационарный нормальный процесс с нулевым
средним значением и корреляционной функцией 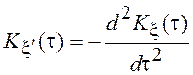 , где
, где ![]() – КФ исходного процесса.
– КФ исходного процесса.
Спектральная плотность процесса x¢(t), как уже отмечалось, равна ![]() ,
где
,
где ![]() – спектральная плотность исходного процесса.
– спектральная плотность исходного процесса.
Результат действия оператора
Вольтерра с ядром ![]() на стационарный нормальный
процесс даст нормальный СП
на стационарный нормальный
процесс даст нормальный СП 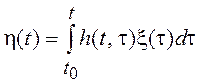 , который в общем
случае уже не будет стационарным. Его среднее значение
, который в общем
случае уже не будет стационарным. Его среднее значение
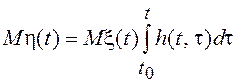
и дисперсия
![]()
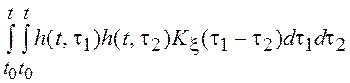 .
.
зависят от времени.
Если t0 = –¥, а ![]() =
= ![]() , что
соответствует установившемуся режиму отклика стационарной линейной системы с
импульсной характеристикой
, что
соответствует установившемуся режиму отклика стационарной линейной системы с
импульсной характеристикой ![]() , то процесс на выходе
можно считать стационарным нормальным процессом со средним значением
, то процесс на выходе
можно считать стационарным нормальным процессом со средним значением 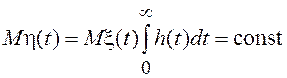 и дисперсией
и дисперсией
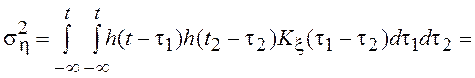
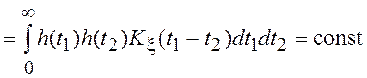 ,
,
не зависящими от времени. Корреляционную функцию можно
найти с помощью обратного преобразования Фурье спектральной плотности выходного
процесса ![]() =
= ![]() , где
, где 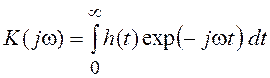 – коэффициент передачи линейной цепи, т.
е.
– коэффициент передачи линейной цепи, т.
е.
![]()
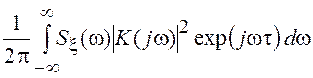 .
.
Часто приходится иметь дело с линейным функционалом вида
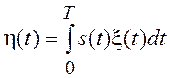 ,
,
где s(t) –
детерминированная функция, x(t) –
стационарный нормальный СП. Как результат линейного преобразования нормального
СП, h является нормальной случайной величиной со средним
значением 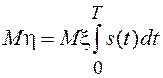 и дисперсией
и дисперсией ![]()
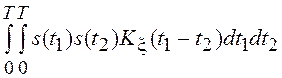 . Если корреляционная функция процесса с
имеет вид
. Если корреляционная функция процесса с
имеет вид 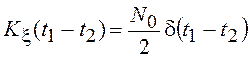 , то
, то ![]() =
= ![]()
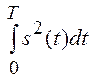 .
.
Как уже отмечалось, процесс с такой КФ называется “белым” шумом по
аналогии с белым светом, имеющим постоянную во всем частотном диапазоне
спектральную плотность мощности ![]() =
= ![]() .
.
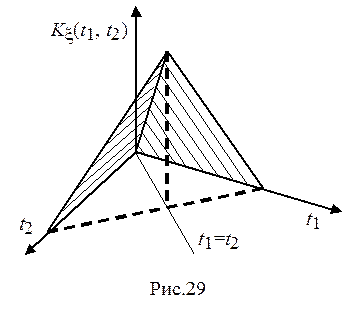 Важной моделью СП с независимыми приращениями (см. классификацию СП)
является винеровский процесс, для которого разность отсчетов
Важной моделью СП с независимыми приращениями (см. классификацию СП)
является винеровский процесс, для которого разность отсчетов
x(t+
t) – x(t) при любом
t имеет нормальное распределение с нулевым средним значением
М[x(t+
t) – x(t)] = 0 и
дисперсией М{[x(t+
t) – x(t)]2}
=![]() . Корреляционная функция Винеровского процесса
. Корреляционная функция Винеровского процесса ![]() , ее график приведен на рис. 29.
, ее график приведен на рис. 29.
Винеровский процесс нестационарен, его часто называют процессом, описывающим броуновское движение частицы под действием ударов молекул жидкости. Производная винеровского процесса является гауссовским (нормальным) “белым” шумом.
Поскольку нормальный СП полностью определяется заданием среднего значения и КФ, которые могут быть вычислены с помощью двумерной ПВ, то задание двумерной ПВ при произвольном расположении отсчетов полностью определяет нормальный СП. Для произвольной двумерной ПВ справедливо представление вида
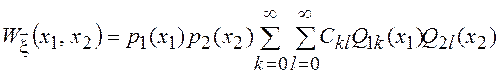 ,
,
где ![]() и
и ![]() – ортонормальные многочлены,
соответствующие весовым функциям
– ортонормальные многочлены,
соответствующие весовым функциям ![]() и
и ![]() . Коэффициенты Стп
находятся с помощью умножения обеих частей записанного равенства на
. Коэффициенты Стп
находятся с помощью умножения обеих частей записанного равенства на ![]()
![]() и двойного
интегрирования по области, определенной весовыми функциями, что с учетом
ортонормальности
и двойного
интегрирования по области, определенной весовыми функциями, что с учетом
ортонормальности ![]() и
и ![]() дает:
дает:
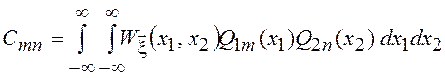 .
.
Так как произведение полиномов ![]()
![]() есть выражение вида
есть выражение вида
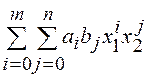 ,
,
то коэффициенты Стп выражаются через
корреляционные моменты mij. В роли весовых функций обычно выступают одномерные
ПВ ![]() и
и ![]() . Для
стационарного нормального СП с нулевым средним значением и единичной дисперсией
выполняются соотношения
. Для
стационарного нормального СП с нулевым средним значением и единичной дисперсией
выполняются соотношения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.