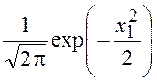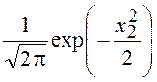
Нормальный случайный процесс, страница 2

= = ,  =  =

и разложение двумерной ПВ имеет вид:

==

=,

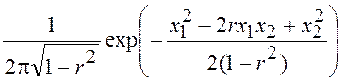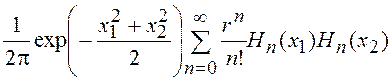где r – коэффициент корреляции отсчетов процесса, а 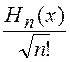 – нормированные полиномы Эрмита, с которыми мы познакомились в гл.6.

Для общего случая двумерного нормального распределения выражение для двумерной ПВ примет вид:

=

.

Узкополосный нормальный случайный процесс

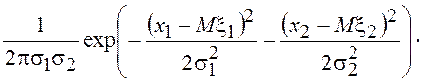
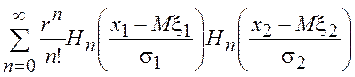Корреляционная функция и связанная с ней спектральная плотность СП были рассмотрены выше. Для узкополосных СП, как и для детерминированных сигналов, весьма продуктивным является представление исходного СП x(t) в виде , где процессы  и  называют  квадратурными компонентами процесса x(t).

Переход от процесса x(t) к огибающей и фазе осуществляется с помощью сопряженного процесса x_^(t), получаемого из исходного с помощью оператора (преобразования) Гильберта:

x_^(t) = Нx(t) = .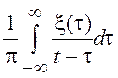

Для существования процесса x_^(t) достаточно потребовать равенства нулю среднего значения процесса x(t), т. е. Мx(t) = 0 при любых t.

С помощью процесса x_^(t) можно построить аналитический СП

= x(t) + j x_^(t) = ,

где комплексная случайная функция  называется комплексной огибающей СП x(t).

Так как , то , т. е. огибающая нигде не пересекает СП x(t). Дифференцируя по t равенство

,

получим , поэтому в тех точках, где = x(t) и, следовательно, x_^(t) = 0, имеет место равенство . Таким образом, случайный процесс  при всех t больше или равен , а в точках соприкосновения (= x(t)) имеет общие с x(t) касательные (). Эти свойства и определяют для  название огибающей СП x(t).

Учитывая, что

;

,

можно записать представление квадратурных компонент a(t) и b(t) через исходный огибающей СП x(t) и процесс x_^(t) в виде:

,

.

При записи этих соотношений было использовано свойство оператора Гильберта «замораживать» медленно меняющиеся сомножители, т.е. , где  - «медленный» множитель, а  - «быстрый» множитель, спектры которых не пересекаются.

Для нормального СП квадратурные компоненты также будут нормальными СП. Доказать справедливость этого утверждения мы предлагаем читателю.

Так как средние значения процессов x(t) и  x_^(t) равны нулю, то также равны нулю и средние значения процессов a(t) и b(t). Их корреляционные функции одинаковы и равны

.

Для стационарного процесса x(t)

, ,

поэтому  , т. е. для нормального стационарного СП квадратурные компоненты будут также стационарными нормальными СП.

Аналогичным образом можно показать, что взаимная корреляционная функция квадратурных компонент определяется выражением:

.

Можно показать, что взаимная корреляционная функция равна

,

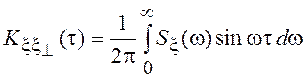где  – спектральная плотность процесса x(t)  и, значит, является нечетной функцией, равной нулю при t = 0 (при совпадении моментов t₁ и t₂).

Таким образом, в совпадающие моменты времени t₁ = t₂ = t квадратурные компоненты узкополосного стационарного нормального процесса x(t) являются независимыми гауссовскими случайными величинами, имеющими нулевые средние значения и дисперсию , равную дисперсии исходного процесса x(t).

Для нахождения ПВ отсчетов огибающей  и фазы  необходимо использовать их связь с отсчетами квадратурных компонент a(t) и b(t), приведенную выше. Из этих соотношений следует, что  есть модуль случайного вектора с декартовыми компонентами a(t) и b(t), а 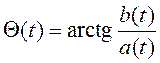 – его аргумент. Учитывая изложенные выше свойства процессов a(t) и b(t), мы приходим к рассмотренной выше задаче о распределении модуля и аргумента нормального случайного вектора с независимыми компонентами, имеющими нулевые средние значения и одинаковые дисперсии . Напомним, что в такой постановке отсчеты огибающей  и фазы  будут независимыми случайными величинами, причем W(r) будет распределением Релея: