Отметим, что суммарный
процесс перестанет быть нормальным, так как ПВ его отсчетов, ПВ суммы
независимых случайных величин, будет являться сверткой нормального
распределения 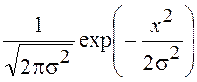 и распределения
и распределения 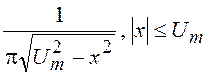 , которому подчиняются отсчеты
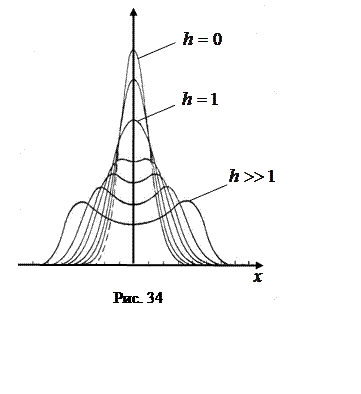
, которому подчиняются отсчеты ![]() при равномерном распределении j в интервале [–p, p]. Вид этого распределения для нескольких значений параметра
при равномерном распределении j в интервале [–p, p]. Вид этого распределения для нескольких значений параметра 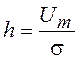 представлен на рис. 34.
представлен на рис. 34.
![]() Во многих задачах возникает необходимость в знании
совместной ПВ отсчетов огибающей и фазы в моменты времени, разделенные промежутком
t. Для решения этой задачи необходимо найти совместную
ПВ отсчетов квадратурных компонент для соответствующих моментов времени, т. е.
Во многих задачах возникает необходимость в знании
совместной ПВ отсчетов огибающей и фазы в моменты времени, разделенные промежутком
t. Для решения этой задачи необходимо найти совместную
ПВ отсчетов квадратурных компонент для соответствующих моментов времени, т. е. ![]() , где
, где ![]() –
отсчеты квадратурных компонент в моменты t и t+ t соответственно.
–
отсчеты квадратурных компонент в моменты t и t+ t соответственно.
Случайные величины ![]() являются совместно
нормальными, поэтому для определения
являются совместно
нормальными, поэтому для определения ![]() с учетом того, что
с учетом того, что ![]()
![]() , необходимо задать
корреляционную матрицу:
, необходимо задать
корреляционную матрицу:
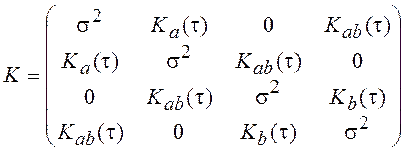 ,
,
где ![]() – равные между собой
корреляционные функции квадратурных составляющих,
– равные между собой
корреляционные функции квадратурных составляющих, ![]() –
взаимная КФ квадратурных составляющих. КФ
–
взаимная КФ квадратурных составляющих. КФ ![]() и
и ![]() были определены выше. При записи
корреляционной матрицы было учтено, что квадратурные составляющие в совпадающие
моменты времени некоррелированы, а
были определены выше. При записи
корреляционной матрицы было учтено, что квадратурные составляющие в совпадающие
моменты времени некоррелированы, а ![]() .
.
Пользуясь правилами
функционального преобразования совокупности случайных величин, можно найти
совместное распределение отсчетов огибающей в моменты t и t + t, r и rt и отсчетов фазы Q и Qt ![]() , а
затем двойным интегрированием по Q, Qt или по r, rt определить
, а
затем двойным интегрированием по Q, Qt или по r, rt определить ![]() или
или
![]() .
.
В результате этих операций двумерная ПВ отсчетов огибающей стационарного узкополосного нормального процесса, разделенных интервалом t, будет иметь вид:
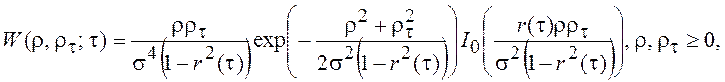
где r(t) – огибающая коэффициента корреляции исходного узкополосного случайного процесса.
Если r(t) = 0, то
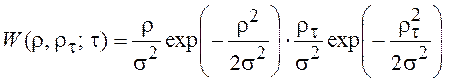
равно произведению ПВ отсчетов огибающей, т. е. r и rt – независимые случайные величины. Однако это не
означает, что из некоррелированности отсчетов исходного узкополосного
нормального процесса ![]() следует независимость отсчетов
огибающей, так как КФ процесса
следует независимость отсчетов
огибающей, так как КФ процесса ![]() , равная
, равная
![]()
может обращаться в нуль за счет второго сомножителя.
При этом ![]() может быть отлично от нуля.
может быть отлично от нуля.
Зная двумерную ПВ огибающей, можно найти КФ
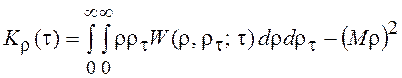 .
.
Записывая представление ![]() с
помощью ортогональных многочленов, в роли которых для данного распределения
будут выступать полиномы Лагерра (см. гл.6), можно получить представление
с
помощью ортогональных многочленов, в роли которых для данного распределения
будут выступать полиномы Лагерра (см. гл.6), можно получить представление ![]() в виде ряда по степеням огибающей
коэффициента корреляции исходного процесса
в виде ряда по степеням огибающей
коэффициента корреляции исходного процесса ![]() . С деталями
можно ознакомиться с помощью [9]. Для коэффициента корреляции огибающей это
даст
. С деталями
можно ознакомиться с помощью [9]. Для коэффициента корреляции огибающей это
даст
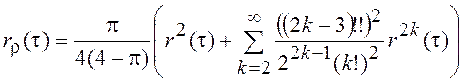 ,
,
где ![]() – произведение
нечетных чисел, начиная с единицы.
– произведение
нечетных чисел, начиная с единицы.
В качестве упражнения на сообразительность читателю
предлагается найти значение 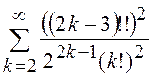 .
.
Так как выражение для ![]() содержит только четные
степени
содержит только четные
степени ![]() и поэтому неотрицательно, то равенство
нулю
и поэтому неотрицательно, то равенство
нулю ![]() возможно только при
возможно только при ![]() = 0. Но, как было показано выше, при
= 0. Но, как было показано выше, при ![]() = 0 отсчеты огибающей независимы. Таким
образом, при
= 0 отсчеты огибающей независимы. Таким
образом, при ![]() = 0 отсчеты огибающей будут независимы и мы
получим еще один пример, когда из некоррелированности случайных величин следует
их независимость. Первый пример был связан с нормальными случайными величинами.
= 0 отсчеты огибающей будут независимы и мы
получим еще один пример, когда из некоррелированности случайных величин следует
их независимость. Первый пример был связан с нормальными случайными величинами.
При квадратичном детектировании выходной сигнал равен квадрату огибающей колебания, поступающего на вход детектора. Пользуясь правилами функционального преобразования случайных величин можно найти одномерные ПВ квадрата огибающей при отсутствии сигнала
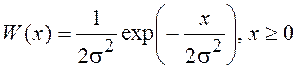
и при наличии гармонического сигнала с частотой w0 и амплитудой Um
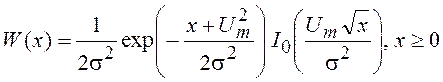 .
.
Для корреляционной функции квадрата огибающей узкополосного стационарного нормального процесса, которую можно получить с помощью двумерной ПВ квадрата огибающей на основе правил преобразования совокупности СВ, справедливо выражение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.