Задача синтеза и анализа дискретного фильтра, страница 7

Чтобы установить вид сигнала на выходе ДФ, необходимо знать его импульсную характеристику h(kТ). Как следует из [1]–[7], она связана с системной функцией H(z) дискретного фильтра z-преобразованием. Поскольку выражение для H(z) уже получено в 3.4, можно воспользоваться формулой обратного z-преобразования [1]–[7], однако ее непосредственное применение вызывает определенные трудности и необходимо в тех случаях, когда нельзя использовать более простые методы, которые в данной ситуации вполне подходят.

В основе предлагаемого метода расчета импульсной характеристики лежит представление системной функции фильтра (2.4) в виде суммы простейших дробей. Чтобы такое представление было возможно, системная функция должна быть правильной дробно-рациональной функцией, т. е. степень числителя должна быть меньше степени знаменателя. Следует обратить внимание на то, что числитель и знаменатель рассматриваются здесь как полиномы относительно переменной z^–1, а не относительно z. В нашем случае это условие не выполняется, поскольку фильтры, синтезированные методом билинейного z-преобразования, имеют одинаковые степени числителя и знаменателя системной функции. Поэтому прежде всего необходимо выделить в системной функции (2.4) целую часть, представив ее в виде

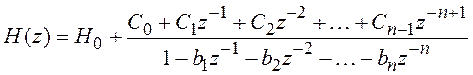                       ,              (3.1)

где , а вещественные коэффициенты , , …,  легко находятся исходя из тождественного равенства выражений (2.4) и (3.1).

Учитывая линейность обратного z‑преобразования и тот факт, что z‑пре­образование от единичного дискретного сигнала , описываемого соотношением (2.1), есть единица, получим, что слагаемому  в выражении (3.1) соответствует слагаемое импульсной характеристики, равное

                                                      .                                             (3.2)

Второе слагаемое в формуле (3.1) является правильной дробно-рациональной функцией относительно  и при отсутствии у знаменателя кратных корней (а для рассматриваемых в данной курсовой работе фильтров это условие всегда выполняется) может быть представлено в виде суммы простейших дробей вида

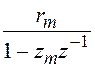                                                       .                                             (3.3)

Здесь  — полюс системной функции (корень ее знаменателя), а  — соответствующий этому полюсу вычет. Для фильтра с вещественными коэффициентами полюсы могут быть также вещественными либо образовывать комплексно-сопряженные пары. То же относится и к вычетам.

Выражение вида (3.3) можно представлять в виде суммы бесконечной геометрической прогрессии:

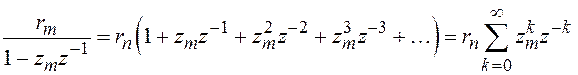              .     (3.4)

Представление (3.3) в форме (3.4) справедливо, если ряд сходится, т. е. при . Сравнивая соотношения (3.4) и (2.3), можно заметить, что сумме ряда соответствует последовательность отсчетов вида

                                                   ,     k ³ 0.                                          (3.5)

Применение соотношения (3.4) к паре комплексно-сопряженных полюсов дает две бесконечные геометрические прогрессии, комплексно-сопря­женные по отношению друг к другу. Сложение прогрессий дает вещественную последовательность, представляющую собой отсчеты экспоненциально затухающей косинусоиды:

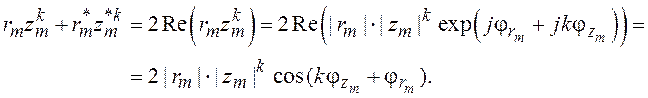         (3.6)

Таким образом, окончательное аналитическое выражение для импульсной характеристики дискретного фильтра описывается суммой слагаемых вида (3.2), (3.5) и (3.6).

Полученное выражение необходимо подвергнуть проверке, состоящей в расчете импульсной характеристики синтезированного фильтра на основе алгоритма его функционирования, записанного в форме (2.2) и использованного в 3.4 при составлении структурных схем дискретного фильтра. Для этого следует принять x(kT) = x₀(kT) и последовательно вычислить несколько отсчетов y(kT) = h(kT) при k = 0, 1, 2, …, которые должны совпасть со значениями, вычисленными для тех же k по аналитической формуле.

Пример. Пусть системная функция H(z) некоторого ДФ третьего порядка представлена в виде

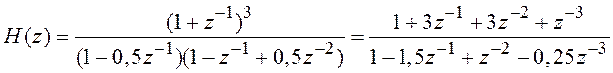            .  (3.7)

1. Из неправильной дроби (3.7) выделяется целая часть, равная отношению коэффициентов при старших (наиболее отрицательных) степенях z, т. е. функция H(z) записывается в форме

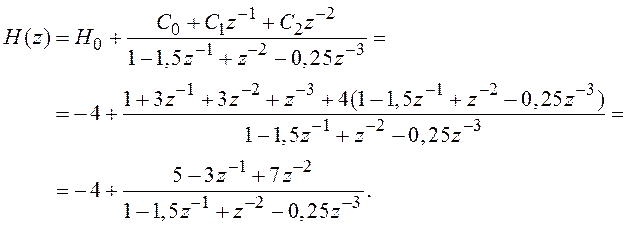             (3.8)