Задача синтеза и анализа дискретного фильтра, страница 2

Импульсной характеристикой h(kТ) дискретного фильтра называется последовательность отсчетных значений, формирующаяся на его выходе при воздействии на вход единичного дискретного сигнала x₀(kT), имеющего вид

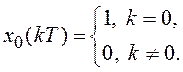                                                                                       (2.1)

Под разностным уравнением дискретного фильтра понимают соотношение, связывающее между собой разности соседних значений входного x(kT) и выходного y(kT) дискретных сигналов. В общем случае оно записывается в форме

                           ,                 (2.2)

где все коэффициенты вещественны.

Применяя к дискретному сигналу x(kТ) преобразование Лапласа и вводя комплексную переменную , можно получить функцию

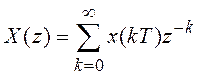                                              ,                                     (2.3)

называемую z‑преобразованием исходного сигнала x(kT).

Системная функция H(z) дискретного фильтра определяется как отношение z‑преобразований его выходного и входного сигналов. Если алгоритм функционирования дискретного фильтра описывается разностным уравнением в форме (2.2), то его системная функция записывается как

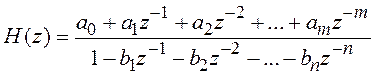                               .                      (2.4)

Существует однозначная связь между системной функцией H(z) и комплексным коэффициентом передачи  дискретного фильтра. Если переход от функции передачи K(p) к комплексному коэффициенту передачи осуществляют заменой комплексной переменной р на мнимую jw, то в рассматриваемом случае, с учетом соотношения z = exp(pT)

                                                ,                                       (2.5)

что указывает на периодический характер частотной характеристики дискретного фильтра.

Среди различных методов синтеза дискретных фильтров особое место занимают такие, которые основаны на применении опыта, накопленного радиоспециалистами при разработке аналоговых устройств соответствующего назначения. Использование аналогового фильтра-прототипа дает возможность синтезировать дискретный фильтр либо исходя из требуемой импульсной характеристики, либо обеспечивая заданную частотную характеристику. В данной курсовой работе реализуется второй, более сложный, вариант синтеза дискретного фильтра. Чаще всего при этом применяется метод билинейного z-преобразования, суть которого требует следующих комментариев. Допустим, что известен вид коэффициента передачи K(р) в операторной форме, который имеет необходимый аналоговый фильтр-прототип (это может быть ФНЧ, полосовой фильтр и т. д.). Подстановкой , вытекающей из определения z-преобразования, легко получить системную функцию H(z) дискретного фильтра, который будет иметь частотную характеристику, в точности совпадающую с исходной характеристикой аналогового фильтра-прототипа. Однако данная системная функция окажется нереализуемой, так как при дробно-рациональном характере K(р) она будет содержать трансцендентные функции. Чтобы добиться физической реализуемости системной функции и одновременно существенно не исказить частотную характеристику фильтра-прототипа, используют разложение зависимости p(z) в ряд по степеням отношения двух линейных функций (билинейного отношения) . При сохранении только первого члена ряда получают следующее соотношение [1]:

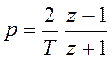                                                     .                                            (2.6)

При подстановке комплексной переменной p в форме (2.6) в выражение для операторного коэффициента передачи фильтра-прототипа получают дробно-рациональную системную функцию H(z). Однако вследствие принятого приближения частотная ось при переходе от аналогового фильтра-прототипа к дискретному варианту трансформируется, а именно: точки частотной характеристики аналогового фильтра, соответствующие текущему значению частоты , будут расположены на частотной характеристике дискретного фильтра на частотах . Связь между данными частотами устанавливается из соотношения (2.6), если положить в нем , а . Она имеет нелинейный характер:

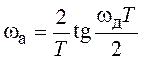                                                   .                                          (2.7)