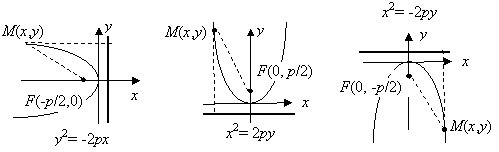Кривые второго порядка на плоскости. Поверхности второго порядка, страница 3

                        .

            Это уравнение называется каноническим уравнением параболы.

            Другие возможные случаи расположения параболы на плоскости и соответствующие канонические уравнения приведены на рисунке справа.

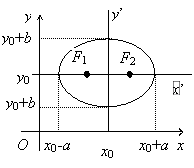
            2.1.7.5. Смещенные кривые второго порядка. Рассмотрим, как преобразуются уравнения эллипса, гиперболы, параболы, если их центры не совпадают с началом системы координат, но оси остаются параллельными координатным осям. Пусть, например, центр эллипса имеет координаты (х₀, у₀). В координатах 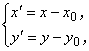 полученных в результате параллельного переноса, уравнение имеет канонический вид 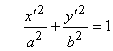. Таким образом, в исходных координатах уравнение смещенного эллипса будет .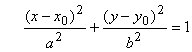

            Для смещенных гипербол уравнения будут иметь вид 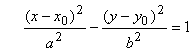 или 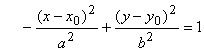; для смещенных парабол , ,  или .

            2.1.7.6. Исследование уравнения второго порядка Ах² + Ву² + 2Dх + 2Ey + F = 0. Кривые, соответствующие этому уравнению. При исследовании этого уравнения будем считать, что коэффициенты А, В не равны нулю одновременно (именно эти коэффициенты определяют тип кривой). Рассмотрим возможные случаи.

            1. Коэффициенты А и В имеют один знак. В этом случае кривую, соответствующую этому уравнению, называют кривой эллиптического типа. Будем полагать, что A > 0, B > 0 (иначе умножим уравнение на -1). Сгруппируем в уравнении члены с х¸ у и выделим полные квадраты ,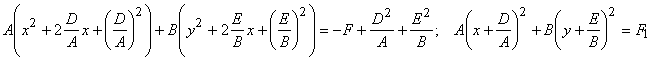

где . Выполним параллельный перенос системы координат: 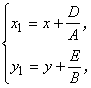 тогда уравнение примет вид .

1.1.  Если F₁ > 0, получаем каноническое уравнение эллипса 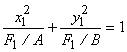 с полуосями .

1.2.  Если F₁ = 0, получаем уравнение . Если A > 0, B > 0, это возможно только при х₁ = 0, у₁ = 0. Таким образом, в этом случае эллипс вырождается в точку х₁ = 0,

у₁ = 0, или х = -D/A, у = -E/B.

1.3.  Если F₁ < 0, получим уравнение 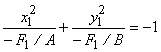. Этому уравнению не может удовлетворять ни одна точка, поэтому говорят, что в этом случае уравнение определяет мнимый эллипс.

2. Коэффициенты А и В имеют разные знаки. В этом случае кривую, соответствующую этому уравнению, называют кривой гиперболического типа. Умножением, при необходимости, на -1, можно всегда сделать A > 0, B < 0. В полученном после выделения полных квадратов уравнении 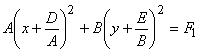 снова возможны три случая.

1.4.  Если F₁ > 0, получаем каноническое уравнение гиперболы 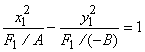 с действительной полуосью , мнимой полуосью .