2.1.7. Кривые второго порядка на плоскости.
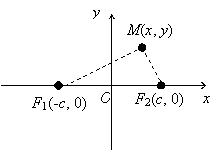 2.1.7.1. Кривыми второго
порядка называют кривые, которые в декартовой системе координат на
плоскости задаются уравнением второго порядка ах2 + by2 + cхy + dx + ey + f = 0 (а, b, c, d, e, f – известные действительные коэффициенты).
2.1.7.1. Кривыми второго
порядка называют кривые, которые в декартовой системе координат на
плоскости задаются уравнением второго порядка ах2 + by2 + cхy + dx + ey + f = 0 (а, b, c, d, e, f – известные действительные коэффициенты).
2.1.7.2. Эллипс. Пусть на плоскости даны две точки F1 и F2, расстояние между которыми равно 2с. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до фокусов постоянна и равна 2а (a > c). Точки F1 и F2 называются фокусами эллипса.
Для того, чтобы получить
уравнение эллипса, введем на плоскости прямоугольную систему координат. Начало
координат совместим со серединой отрезка F1F2, ось Ох направим вдоль этого
отрезка, ось Оу – перпендикулярно ему. Тогда фокусы имеют координаты F1(-c, 0) и F2(c, 0), и
если M(x, y) – текущая точка эллипса, то расстояния от этой точки
до фокусов равны длинам фокальных радиусов F1M и F2M:![]() и
и ![]() . Определение эллипса запишется так:
. Определение эллипса запишется так: ![]() . Преобразуем это уравнение, чтобы избавиться
от корней:
. Преобразуем это уравнение, чтобы избавиться
от корней: ![]()
![]()
![]()
![]()
![]()
![]() .
.
Введем еще один параметр эллипса
соотношением ![]() . Тогда последнее уравнение запишется
как
. Тогда последнее уравнение запишется
как ![]() , и после деления на правую часть
окончательно получим
, и после деления на правую часть
окончательно получим
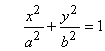 .
.
Это уравнение называется каноническим уравнением эллипса.
Исследуем это уравнение.
1.  Понятно, что
Понятно, что
![]() .
.
2. Так как в уравнение входят только четные степени х, у, то если точка (х, у) принадлежит эллипсу, т.е. х, у удовлетворяют уравнению, то точки (-х, у), (х, -у), (-х, -у) тоже принадлежат уравнению. Следовательно, оси Oх и Оу являются осями симметрии эллипса, точка О(0, 0) является центром симметрии.
3. Рассмотрим
часть эллипса, расположенную в первом квадранте (![]() ).
Решив уравнение относительно у, получим
).
Решив уравнение относительно у, получим 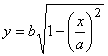 .
Если x = 0, то у = b;
у убывает при возрастании х; если x
= а, то у = 0.
.
Если x = 0, то у = b;
у убывает при возрастании х; если x
= а, то у = 0.
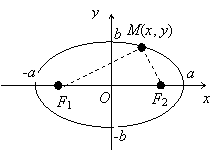
На рисунке справа изображена кривая, имеющая эти свойства. Это и есть эллипс.
Число а
называют большой полуосью эллипса, b – малой полуосью.
Число ![]() называется эксцентриситетом эллипса.
Этот параметр характеризует «сплюснутость» эллипса. Если
называется эксцентриситетом эллипса.
Этот параметр характеризует «сплюснутость» эллипса. Если ![]() (т.е. с = 0, b = а) фокусы эллипса
совпадают с его центром, полуоси равны и эллипс превращается в окружность. Если
(т.е. с = 0, b = а) фокусы эллипса
совпадают с его центром, полуоси равны и эллипс превращается в окружность. Если
![]() (
(![]() )
эллипс вырождается в отрезок, соединяющий фокусы.
)
эллипс вырождается в отрезок, соединяющий фокусы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.