Кривые второго порядка на плоскости. Поверхности второго порядка, страница 2

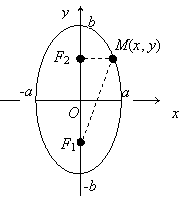
Эллипс может быть расположен так, что большая полуось расположена на оси Оу. В этом случае фокусами являются точки F₁(0, -c) и F₂(0, c), точка M(x, y) удовлетворяет уравнению | F₁M | + | F₂M | = 2b, малая полуось , эксцентриситет , каноническое уравнение остается тем же .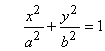

   2.1.7.3. Гипербола. Здесь также задаются две точки F₁ и F₂  (фокусы гиперболы), расстояние между которыми равно 2с, и гипербола определяется как геометрическое место точек плоскости, для которых разность расстояний до фокусов по модулю постоянна и равна 2а (a < c). Уравнение || F₁M | – | F₂M || = 2a в координатной форме запишется как . Преобразуем:

  параметр b гиперболы вводится соотношением , каноническое уравнение гиперболы имеет вид

. .

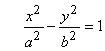            Из этого уравнение следует, что

1. ;

2.  И здесь в уравнение входят только четные степени х, у, поэтому оси Oх и Оу являются осями симметрии эллипса, точка О(0, 0) является центром симметрии.

3.  В первом квадранте 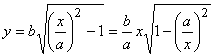. Если x = а, то у = 0; у возрастает вместе с х. При больших функция  - бесконечно малая, и ей можно пренебречь, т.е. прямая  является наклонной асимптотой при  (строго это можно показать методами математического анализа).

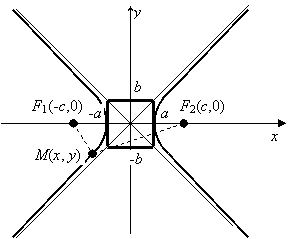
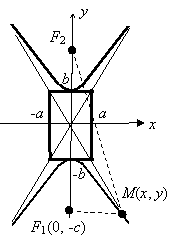Кривая, имеющая эти свойства, изображена  на рисунке справа. Вследствие симметрии прямая  является асимптотой гиперболы и  при , по той же причине прямая  также является двусторонней асимптотой. Параметр а называют действительной полуосью гиперболы, параметр b –мнимой полуосью. Число  называется эксцентриситетом гиперболы. Так как a < c, то .

Фокусы гиперболы могут быть расположены на оси Оу: F₁(0, -c),

F₂(0, c). В этом случае точка M(x, y) гиперболы будет удовлетворять уравнению || F₁M | – | F₂M || = 2b, b < c, параметр а вводится соотношением , , действительная полуось гиперболы будет равна b, мнимая – а, каноническое уравнение примет вид .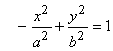

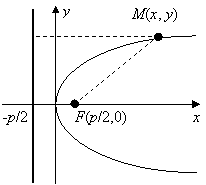            2.1.7.4. Парабола. На плоскости задана точка F (фокус параболы) и прямая (директриса параболы). Расстояние между фокусом и директрисой равно р (параметр параболы). Параболой называется геометрическое место точек M(x, y) плоскости, для которых расстояние до фокуса равно расстоянию до директрисы. Если расположить начало системы координат посередине между фокусом и директрисой, ось Ох направить перпендикулярно, ось Оу – параллельно директрисе, то в координатной форме условие определения запишется так: 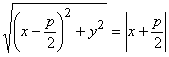. После возведения в квадрат получим