Кривые второго порядка на плоскости. Поверхности второго порядка, страница 4

1.5.  Если F₁ = 0, получаем уравнение . Если A > 0, B < 0, это уравнение пары пересекающихся прямых . Можно считать, что в этом случае гипербола вырождается в асимптоты.

1.6. Если F₁ < 0, получим уравнение 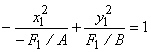. Это уравнение гиперболы с мнимой полуосью ,  действительной полуосью .

3. Один из коэффициентов А, В равен нулю. Будем считать для определенности, что A > 0,    В = 0. Уравнение Ах² + 2Dх + 2Ey + F = 0 представим в виде 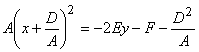 . Возможны случаи:

            3.1.  Е = 0. 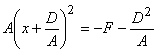. Если правая часть этого уравнения положительна 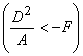, то 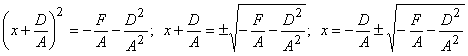, т.е. уравнение определяет пару параллельных между собой и оси Оу прямых. Если правая часть равна нулю, получаем пару совпавших прямых . Если правая часть отрицательна, получится пара мнимых прямых.

            3.2. . Приведем уравнение к виду 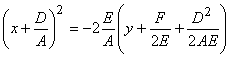. Если , , 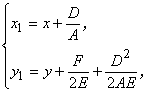получаем каноническое уравнение параболы .

2.1.8. Поверхности второго порядка.

            2.1.8.1. Поверхностью второго порядка называется множество точек пространства, которое в декартовой системе координат определяется уравнением

                        а₁₁х² + а₂₂у² + а₃₃z² + 2а₁₂хy + 2а₁₃хz + 2а₂₃yz + 2b₁х + 2b₂y + 2b₃z + с = 0.

            2.1.8.2. Цилиндрические поверхности второго порядка. Пусть в пространстве задана прямая l и кривая L, не являющаяся прямой, параллельной l. Цилиндрической поверхностью называется поверхность, образованная множеством прямых, параллельных l и проходящих через точки L. Кривая L называется направляющей цилиндрической поверхности; прямые, параллельные l, из которых состоит поверхность, называются образующими цилиндрической поверхности.

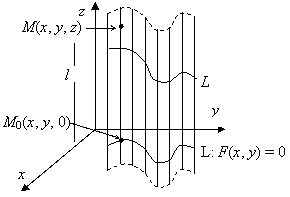
            Введем в пространстве декартову систему координат так, чтобы ось Oz была параллельна прямой l (и, как следствие, образующим поверхности). Будем считать, что пересечение поверхности с плоскостью Оху определяет кривую L, имеющую уравнение F(x, y) = 0. Если этому уравнению удовлетворяет точка M₀(x, y, 0), принадлежащая кривой L, то ему удовлетворяет любая точка M(x, y, z) при любом z (так как координата z в уравнении в явном виде отсутствует), т.е. любая точка образующей. Таким образом, уравнение F(x, y) = 0 определяет всю цилиндрическую поверхность. Доказана

            Теорема. Любая цилиндрическая поверхность с образующими, параллельными оси Oz, определяется уравнением F(x, y) = 0. Обратно, любое такое уравнение задает цилиндрическую поверхность с образующими, параллельными Oz.