Математика \ Высшая математика

Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 8

               На рисунках схематически изображены функции, имеющие в (×)х0 разрывы первого и второго рода.

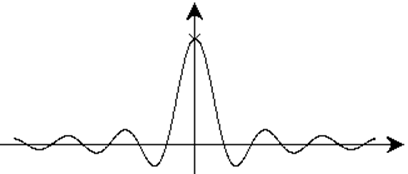
Устранимый разрыв первого рода в точке х0=0.

Здесь изображен график функции ,   х=0 является точкой устранимого разрыва первого рода, так как в точке х=0 функция не определена,  а   .

20

Вариант 2.

1. Построить один из возможных вариантов графика функции у=f(х), для которой , , , .

2. Вычислить

, , ,

, , .

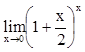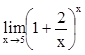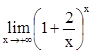3. Найти точки разрыва, асимптоты, интервалы монотонности и экстремумы функций , . Построить графики функций.

4. Вычислить приближенно , используя пять слагаемых в формуле Тейлора. Сравнить с точным значением.

5. Вычислить по формуле Ньютона-Лейбница , .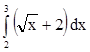

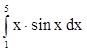6. Составить любую интегральную сумму при n=4 для интегра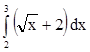ла . Сравнить ее значение с точным значением интеграла.

7. Найти  в произвольной точке и точке М0 (-1,3,3), если .

8. Найти экстремумы функции .

9. Цены на товар три раза повышались на 3%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?

10. Банк выплачивает клиентам 10% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.

57


Df(х0)=.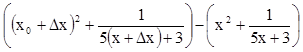

Значение Dх называют приращением аргумента.

Иногда Df(х0) записывают в виде:

Df(х0)=f(х1)-f(х0).                                              (3)

Сравнивая (2) и (3), легко увидеть, что здесь Dх= х1- х0.

Например, Df(1)=f(1,2)-f(1) является приращением f(х) в в (×)х0=1 с Dх=0,2.

               Функция y=f(х) называется непрерывной в точке х0, если приращение функции в этой точке стремится к нулю при стремлении к нулю приращения аргумента

=0.                                  (4)

Легко видеть, что равенство (4) тождественно равенству (1).

1.7 Производная.

1.7.1 Определение производной, таблица производных.

               Производной функции y=f(х) называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

               Производная функции обозначается , или , или , или .

.                               (1)

Приведем пример вычисления производной с использованием (1):

Пусть у(х)=х2.

Тогда .

               Равенство (1) позволяет получить значение производных любых функций, заданных аналитически, но редко используется при нахождении производных. С помощью этого равенства получают производные всех элементарных функций и правила дифференцирования (процесс нахождения производных часто называют дифференцированием).

               Приведем основные правила дифференцирования, обозначая: С – постоянная величина; u(х), v(х) – функции; ,  - их производные по переменой х.

22

my=700×m=350 и 13.23.

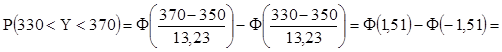
0,8689.

Центральная предельная теория иногда формулируется не для суммы одинаково распределенных случайных величин, а для их среднего арифметического:

Если Х1, Х2, …, Хn – независимые случайные величины, имеющие одно и то же распределение с математическим ожиданием m и дисперсией s2, то при увеличении n закон распределения их среднего арифметического  неограниченно приближается к нормальному с математическим ожиданием  и   (при n®¥ ®0, т.е. среднее арифметическое практически перестает быть случайным и совпадает с М(Х)).

Примечание.

1.  "Методические указания", предлагаемые вниманию студентов, не заменяют учебник.

2.  В "Методических указаниях" отсутствует материал, необходимый для решения задач №№7, 8 по математическому анализу и задач №№ 11, 12 по теории вероятностей.

3.  Материал по комбинаторике, элементам математической логики и процентам находятся в первой части "Методических указаний".

55



           (11*)

 (11**)

                    (12*)

         (12**)

               (13*)

     (13**)
Скачать файл