В этой формуле для получения ответа требуется вычислить значения некоторой функции всего в двух точках. Сложность заключается лишь в нахождении первообразной. Кроме того, формула (6) дает точное значение интеграла, в то время как любая интегральная сумма, строго говоря, дает лишь его приближенное значение.
Покажем применение формулы Ньютона-Лейбница на примерах.
Пример 1.
Вычислить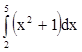 
Решение:
- найдем неопределенный интеграл 
, пользуясь таблицей неопределенных
интегралов или собственной фантазией: 
.
(полученный результат легко проверить: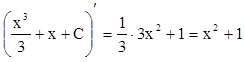 
)
- теперь находим точное значение искомого интеграла
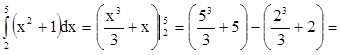42.
Ответ: 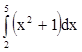=42.
Сравним точное значение интеграла с его
интегральной суммой 
43,515, полученной выше. Разность
между ними равна 0,485, что составляет 1,16% от точного значения. Можно
ожидать, что для этого интеграла интегральная сумма 
практически
совпадет с его точным значением.
37
m=3 (благоприятных исходов здесь три, у нас три черных шарика).
Ответ:
р=
=0,375.
Пример 2.
В урне 5 белых и 3 черных шарика. Наугад вынимают два шара. Найти вероятности того, что: 1) шары разного цвета; 2) оба шара – белые; 3) шары одного цвета (или оба белые, или оба черные).
Решение:
n
(количество способов выбрать два шара из восьми
имеющихся)
m1
(количество способов вынуть один белый и один
черный шар; вычисляется по правилу произведения)
m2
m3
(количество способов вынуть или два
белых шара, или два черных вычисляется по правилу суммы)
Ответ: р1
;
р2
; р3
.
Пример 3.
Брошены две монеты. Найти вероятность того, что выпадут 1) два герба; 2) две решки; 3) герб и решка.
Решение:
n=4 (возможные исходы: ГГ, ГР, РГ, РР) при решении этой задачи часто допускается ошибка, принимают n=3, что не является правильным.
m1=1, m2=1, m3=2.
Ответ: 
, 
, 
.
Пример 4.
В колоде 52 карты. Вынимают 4 карты. События:
А – вынуты 4 туза;
В – вынуты карты одной масти;
С – среди четырех карт – хотя бы один туз;
D – вынуты карты одного цвета;
Е – среди карт – хотя бы одна черная.
1) Найти вероятность данных событий. 2) Дать
описание событий А×В, АС, А+С, 
, ×В, 
×Е и найти их вероятность.
42
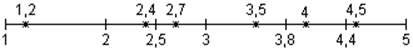
- вычисляем f(х)=х2+1 в выбранных точках (вид функции f(х)=х2+1 определен условием задачи, f(х) – функция, стоящая под знаком интеграла)
|
f(x1)=1,22+1=2,44 |
f(x4)=3,52+1=13,25 |
|
f(x2)=2,42+1=6,76 |
f(x5)=42+1=17 |
|
f(x3)=2,72+1=8,29 |
f(x6)=4,52+1=21,25 |
- составляем интегральную сумму 
2,44×1+6,76×0,5+
+13,25×0,8+17×0,6+×21,25×0,6=43,515
Ответ: одна из интегральных сумм для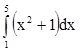 
при n=6 равна 43,515.
Пример 2.
Составить интегральную сумму для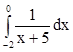 
при n=4, n=20, n=40.
Решение:
1. n=4
- разбиваем промежуток [-2, 0] на четыре части; для удобства – на равные части (разбивать промежуток на равные части не обязательно, но удобно)
- находим Dх1, Dх2, Dх3, Dх4; при разбиении на равные части длины всех частей равны Dх1=Dх2=Dх3=Dх4=0,5
- выбираем точки xi в каждой части; для удобства точку x1 помещаем в середине первой части, точку x2 в середине второй части и т.д.
x1=-1,75, x2=-1,25, x3=-0,75, x4=-0,25
- вычисляем f(х)=
в выбранных точках (вид функции f(х)= определен условием задачи, f(х) –функция, стоящая
под знаком интеграла)
|
f(x1)= |
f(x3)= |
35
2.3 Случайная величина.
Результаты стохастического эксперимента мы называли элементарными исходами и формировали из них случайные события. Если каждому результату стохастического эксперимента, т.е. каждому элементарному исходу поставить в соответствие число, то результатом эксперимента будет случайная величина, т.е. величина, принимающая то или иное значение.
Случайные величины делятся на два типа: дискретные и непрерывные. У дискретных величин множество значений конечно или счетно, т.е. значения дискретной случайной величины можно пронумеровать в каком-то порядке. Для таких величин закон распределения, т.е. правило, позволяющее находить вероятности всевозможных событий, связанных со случайной величиной, чаще всего задают в виде ряда распределения, т.е. таблицы вида:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
