Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 10

достаточно мало) расчеты можно вести по формулам закона Пуассона.

а=nр=2, следовательно,

1) Р(Х=0)=0,135

2) Р(Х³1)=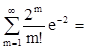1- Р(Х=0)=0,865

3) Р(Х=2)= 0,271

4) Р(Х³3)=

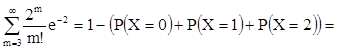
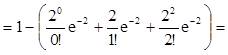0,323

Здесь можно было бы пользоваться формулами биномиального

51

1.7.3 Производные высших порядков.

            Пусть функция y=f(х) имеет производную = на некотором множестве Х и эта производная сама является новой функцией от х .Может случиться, что эта новая функция в свою очередь имеет производную: производную от . Производную от  называют производной второго порядка или второй производной функции y=f(х) и обозначают одним из символов: , , , .

= или .                                 (2)

Например:

                 

                  .

(Заметим, что производную = часто называют производной первого порядка.)

               Аналогично, если функция y=f(х) имеет вторую производную  на некотором множестве Х, то производная от второй производной, если она существует, будет называться производной третьего порядка или третьей производной функции y=f(х). Переходя подобным образом от третьей производной к четвертой и т.д., введем понятие производной n-ого порядка или n-ой производной исходной функции y=f(х), для обозначения которой применяются символы , , , .

               Производной n-ого порядка называют производную от ее (n-1)-ой производной.

= или .                                             (3)

Для того, чтобы найти производную n-ого порядка функции y=f(х), нужно последовательно находить первую, вторую, третью и т.д. производные.

Пусть, например, требуется найти пятую производную функции у(х)=х×cos2x. Тогда

28

F(х)=,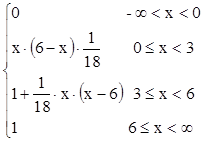

т.е. ее график

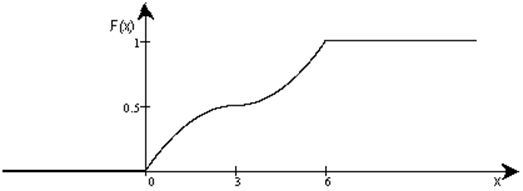
- непрерывная функция, то случайная величина Х распределена непрерывно с плотностью распределения

f(х)=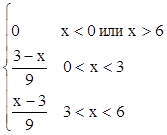

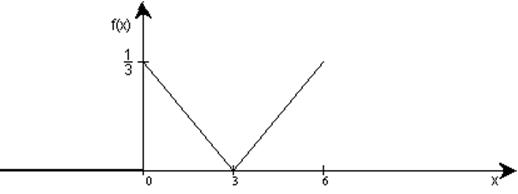
Все значения ХÎ[0, 6],

49

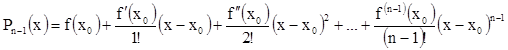  (4)

Этот многочлен P_n-1(x) и его производные до (n-1)-ой включительно в точке х₀ имеют те же значения, что и функция y=f(х).

               Доказано, что в произвольной точке хÎХ разность между значениями функции и многочлена равна

,

где (×)с находится между х и х₀, т.е. при x > х₀ точка с Î (х₀; х), при x < х₀ точка с Î (х; х₀).

Следовательно, в том случае, когда значение выражения  не превышает по абсолютной величине какого-то малого числа e, можно искать значение функции в произвольной точке хÎХ по приближенной формуле

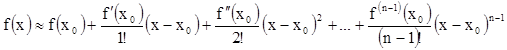   (5)

               Если точку х₀ выбрать так, чтобы значения f(x₀), , , ...,  были известны, можно вычисление значений функции y=f(х) с заданной точностью в произвольной точке х свести к четырем арифметическим действиям: сложению, вычитанию, умножению и делению.

Пример 1.

Вычислить значения ln1,2 с точностью до семи знаков после запятой.

Решение:

1. Рассмотрим функцию у= lnх.

2. Выберем х₀=1, х=1,2.

3. Найдем производные первого, второго и т.д. порядков от функции у=lnх и вычислим их значения в точке х₀=1.

30

возможность вычислять вероятность любых событий, связанных со случайной величиной. Однако во многих практических вопросах нет необходимости в таком полном описании. Достаточно бывает указать только отдельные параметры, характеризующие существенные черты распределения. Например, какое-то среднее, вокруг которого разбросаны значений случайной величины, какое-то число, характеризующее величину этого разброса ("степень случайности" случайной величины) и т.п. Наибольшую роль играют:

1) математическое ожидание случайной величины М(Х)

Математическое ожидание часто называют средним значением случайной величины и иногда обозначают m_x.

2) дисперсия случайной величины D(X)

Иногда D(X) обозначают .

Дисперсия случайной величины есть характеристика рассеивания

случайной величины около ее математического ожидания. Для случайной величины Х, которая принимает единственно возможное значение а, и которая по сути дела не является случайной, М(Х)=а, D(X)=0. Зная m_x=М(Х) и  можно составить приближенное представление о диапазоне ее возможных значений, а именно: значения Х только изредка выходят за пределы интервала , а в большинстве случаев можно считать, что они укладываются в этот интервал.