Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 6

          Выходная случайная величина y представляется как:

          Y = j(X₁,X₂,...,X_k )   +     (X₁,X₂,...,X_k ) ,                 

где  j(X₁,X₂,...,X_k )  -  выборочная функция,

      e (X₁,X₂,...,X_k )  -  случайная составляющая (ошибка).

          Регрессионная  зависимость  определяется  условным  математическим  ожиданием:        М[Y| х₁,х₂,...,х_{k к}] = j( х₁,х₂,...,х_k).

Простейшей зависимостью является линейная зависимость y от одной переменной x:         

          Задача линейного регрессионного анализа заключается в расчете коэффициента а и b, наилучшим образом соответствующих результатам эксперимента. К линейным задачам могут быть приведены и некоторые нелинейные задачи за счет, например, операции логарифмирования.

          Нелинейная зависимость

          y = а х^b переходит в  lg y = lg a + b lg x

          y = e^a+bx переходит в  ln y = a + b x

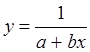             переходит  в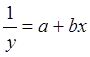            

          Решение таких нелинейных регрессионных задач сводится к решению линейных задач. Графики нелинейных характеристик, которые могут быть сведены к линейным, приведены на рис.8.

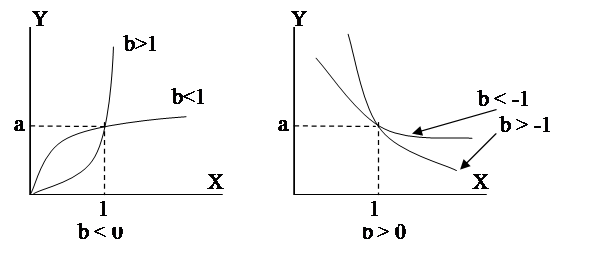
          1) y =ax^b ;     lg y = lg a +b lg x;

 

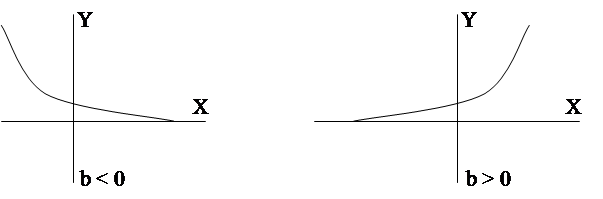
          2)  y = e^a+bx ;    ln y = a + bx ;

                                                                                               

Y

          3)  y =               

%

Y

X

                                                                                             

                                                                                     

X

                                                      

b > 0, a < 0                                           b < 0, a < 0

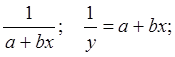
                                                                 рис.8.

                    Нелинейные зависимости приводимые к линейным.

          Решение задач регрессионного анализа обычно реализуется с помощью метода наименьших квадратов (МНК).

          3.1.Метод наименьших квадратов.

          Так как величина  y вычисляется всегда с некоторой ошибкой  e, то можно вычислить среднее квадратичное отклонение:

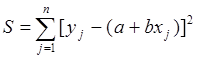
          При использовании МНК среднеквадратичное отклонение должно стремиться к минимальному. Так как функция S зависит от а и b, нужно выбрать такие a и b, чтобы    т.е.

 

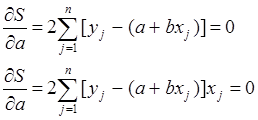          Эта система называется системой нормальных уравнений. Отсюда найдем оценки коэффициента      и коэффициента    .

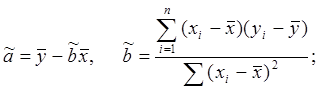           где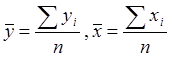 

          При этом оценка дисперсии ошибки :

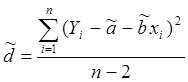
          Можно определить доверительный интервал, и другие гипотезы относительно коэффициентов   и  , так как ниже приведенные значения  t_a и t_b распределены по закону Стьюдента с (n – 2) степенями свободы.

 

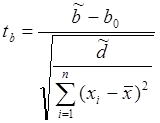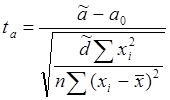                                 -  сравнивается                                                 - сравнивается   

                                    с  t_0,975(n – 2)                                                     с t_0,975(n – 2)

          3.2.Модель множественной линейной регрессии.

          Если число входных величин  x_i  равно  р > 1, то результаты n измерений выходной величины y имеют вид:

          y _j = a₀ + a₁x_1j + a₂x_2j + … + a_px_pj + e_j ,

где   e   - ошибка измерения.

          Эту зависимость удобно представить в векторно матричной форме. Обозначим векторы – столбцы оценок коэффициентов  , вектор результатов измерений , вектор ошибок   :

          Матрица значений x_{i j} называется матрицей плана эксперимента

 

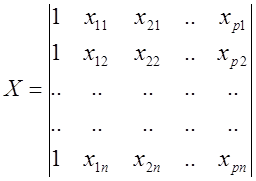          Уравнение множественной линейной регресии в матричной форме имеет вид:

           , откуда   .