Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 4

          Номинальные переменные – переменные, позволяющие разбивать исследуемые объекты на некоторые классы, например, профессия работника, отрасль промышленности.

          2.1.Статистические характеристики, устанавливающие связь между числовыми переменными (при линейной связи x и y).

Обычно статистическая связь между случайными величинами x и y  может характеризоваться с помощью:

α₁₁ = М[XY] – корреляционного момента.

                 = M[(X-m_x)(Y-m_y)]  - ковариационного момента..

          При статистическом анализе обычно пользуются нормированной характеристикой, называемой коэффициентом корреляции r.

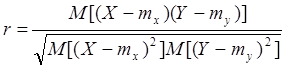
          Если статистическая связь полная, то  

          Если статистическая связь отсутствует, то r = 0.

          Строго говоря, коэффициент корреляции r позволяет судить о степени статистической связи только при  линейной связи X и Y(рис.5.а). Поэтому при r= 0 говорят об отсутствии корреляции между X и Y (а не об отсутствии статистической связи). Для оценки коэффициента корреляции используют следующее соотношение:

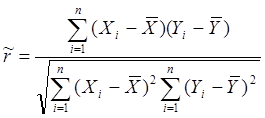,  где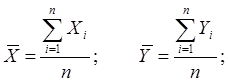    

          Коэффициент корреляции – представляет собой случайную величину, которая при больших  n  имеет распределение, близкое к нормальному,

с дисперсией

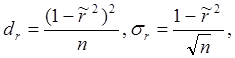
и математическим ожиданием

Таким  образом,  доверительный интервал 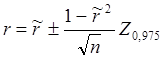  , где  Z_0,975 – 97,5 процентиль нормального [N(0,1)]  распределения.

          Проверка гипотезы об отсутствии статистической связи между x и y осуществляется как обычно:

          Н₀ :    при 

          Н₁ :    при  

 где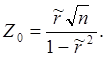                                                  

          2.2.Установление связи между числовыми переменными при нелинейной связи  X  и  Y (корреляционное отношение).

          Если зависимость выходной переменной от входной характеризуется некоторой нелинейной зависимостью, то даже при вполне очевидной связи x и y коэффициент корреляции может равняться нулю, что свидетельствует как-будто об отсутствии статистической связи (рис.5.в).

          В этих случаях возникает необходимость использования не коэффициента корреляции, а так называемого корреляционного отношения. Для нахождения корреляционного отношения разбивают ось x на ряд участков (разрядов).

 

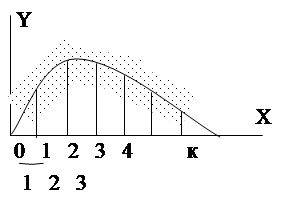рис.6.

                    Выделение  к  разрядов для переменной  x

          Если число точек, определяющих результаты эксперимента на каждом из разрядов равно m_i, то частное среднее для каждого из соответствующих разрядов определяется: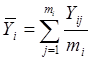  

          Дисперсия средних равна: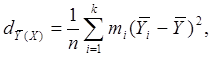  

где    - полное среднее  

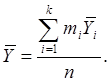
          Для характеристики статистической связи используется корреляционное отношение:

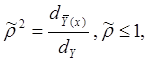
где   .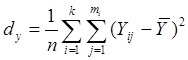    

          Найденное  т.о. корреляционное отношение оказывается близким к нулю при отсутствии статистической связи.   = 1 при полной статистической связи между переменными x и y.

          Для установления факта отсутствия статистической связи используют соотношение: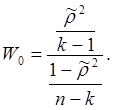  

Эта величина имеет распределение  Фишера с (к – 1) степенями свободы числителя и (n – k) степенями свободы знаменателя. Таким образом, для решения вопроса об отсутствии статистической связи (Н₀:   = 0) используется 95 процентиль этого распределения  W_0,95 (к – 1, n – к). При W₀ < W_0,95 (k – 1, n – k) статистическая связь отсутствует. В противном случае выполняется альтернативная гипотеза  Н₁.

          2.3.Множественный коэффициент корреляции.

          Если рассматривать связь между несколькими входными величинами х и одной выходной величиной  y (рис.7), то   y = j( х₁,х₂,...,х_n )

 

рис.7.                  

         Многомерная система

          При линейной зависимости, эта связь определяется следующей регрессионной зависимостью:

         

Определим, существует ли связь между входными величинами x_i  и выходной величиной y.

          Это осуществляется с помощью множественного коэффициента корреляции. Представим  дисперсию  вышеприведенного  условного  математического  ожидания

в виде   :   

где   - множественный коэффициент корреляции.