Построение математических моделей исследуемых систем на основании экспериментальных данных, страница 2

Полученная с помощью некоторой выборочной функции    = j(X₁,X₂,...,X_n )

конкретная оценка     = j( х₁,х₂,...,х_n )    параметра  a  не дает, однако, возможности судить о том, как точно найденная оценка воспроизводит истинное значение параметра  а, даже если она  является несмещенной  и эффективной. Однако можно найти некоторую область, которая с заданной вероятностью  (обычно 95% или 99%) содержит истинное значение параметра  a.

          Так, например, 95% доверительный интервал для оценки   составляет

               

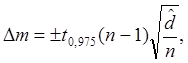
где  - 97,5 процентиль распределения Стьюдента  с n-1  степенями свободы.

          95% доверительный интервал для оценки вероятности случайного события  

определяется  как  

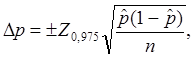
где   Z_0,975  -  97,5  процентиль нормального распределения N(0,1).

          95% доверительный интервал для оценки дисперсии        находится:

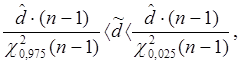
где     и   -  соответственно  97,5 и 2,5 процентиль распреде-ления   χ²    .

          1.3.Статистическая проверка гипотез.

          Наряду со статистической оценкой параметров, задачи проверки гипотез составляют один из важнейших разделов математической статистики.

          Статистическая гипотеза – это утверждение относительного одного или нескольких параметров генеральной совокупности, полученное на основании выборки. Введем обозначения :

          Н₀ – основная гипотеза,

          Н₁ – альтернативная гипотеза.

          При исследовании случайных величин каждое утверждение нельзя сделать однозначно. Поэтому исследуется вероятность выполнения гипотезы Н₀ или альтернативной гипотезы Н₁ .

          Область в которой выполнение гипотезы Н₀ маловероятно, называется критической (рис.4).

 

                        

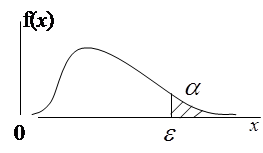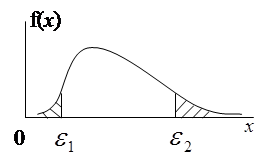
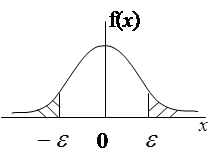
                    а)                                         б)                                         в)

                                      рис.4.

          Характерные виды критических областей (заштрихованы):

          а) симметричная критическая область;

          б) квазисимметричная критическая область;

          в) односторонняя критическая область;

          Для определения величины критической области вводим понятие об ошибке при выполнении гипотезы Н₀. Ошибка первого рода имеет место в случае, если будет принята гипотеза Н₁, хотя на самом деле справедлива гипотеза Н₀.

          Вероятность ошибки первого рода определяется как уровень значимости α.

Обычно  α   принимается равным  1%  или  5% . Таким образом вероятность того, что имеет место Н₀ при заданном уровне значимости определяется :

                Р(Н₀) = 1 - α

          1.3.1.Проверка гипотезы о вероятности случайного события

          При малом числе экспериментов отклонение оценки от истинного значения может  быть  очень большим, а  при  большом должно быть малым. Например, если  Р₀ – вероятность  некоторого случайного события, а в результате эксперимента получена реализация оценки оценка   > p₀ , то этот результат может являться следствием случайного отклонения, поэтому выдвигаем основную гипотезу: 

          Н₀ : p = p₀

          В этом случае альтернативной гипотезой Н^­₁ является гипотеза о том, что результаты опыта свидетельствуют о действительном увеличении вероятности рассматриваемого случайного события.

          Н₁ : р > р₀

          Так как распределение отклонения  ( - р₀ ) – соответствует нормальному распределению, то при уровне значимости  α  =  0,05 (односторонняя критическая область рис.4.в). Находим :

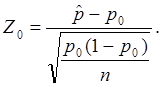
          Если Z₀ < Z_0,975 справедлива гипотеза Н₀, при Z₀ > Z_0,975 справедлива гипотеза Н₁, где Z_0,975 – 95-ая  процентиль нормального N(1,0) распределения.

          Если в результате  n  экспериментов получена оценка   <  р₀, аналогично выдвигаем гипотезу 

          Н₀ :  р = р₀ ,

т.е. полученное отклонение несущественно (случайно). Очевидно эта гипотеза справедлива, если   или   ввиду симметрии нормального распределения. Альтернативная гипотеза   Н₁ :  р < р₀ справедлива при  >  Z_0,975 .