Расчет системы автоматического управления электроприводом при диапазоне регулирования D = 60 и перерегулировании скорости: σ = 25 %, страница 2

Передаточная функция САУ в разомкнутом состоянии по управляющему воздействию определится:

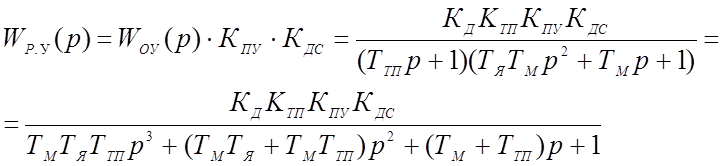
Преобразуем исходную структурную схему к следующему виду:

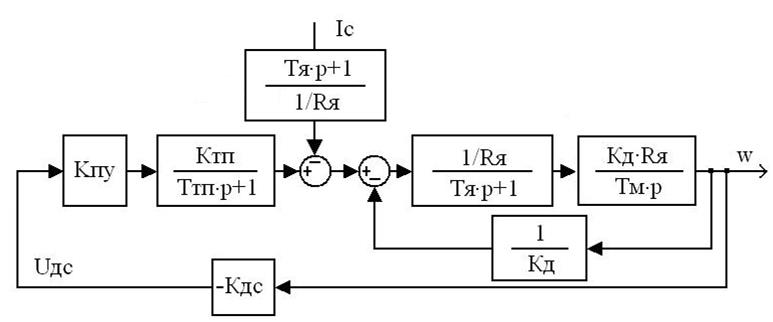
Рисунок 1.2.1 – Преобразованная структурная схема, необходимая
для нахождения передаточных функций по возмущению.

          Передаточная функция разомкнутой системы по возмущающему воздействию:

1.3. Определение требуемого коэффициента усиления
разомкнутой системы из условия статической точности САУ.

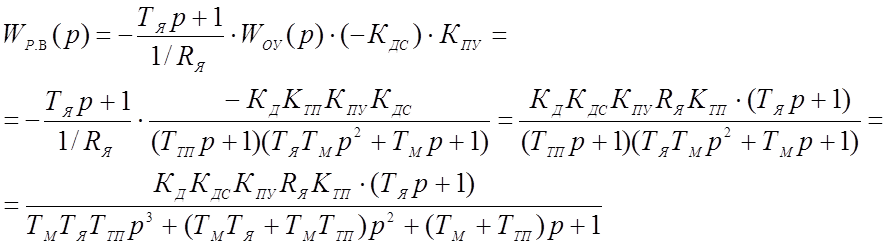
Из условия статической точности (δ = 2%) и заданного диапазона регулирования (D = ω_max/ ω_min= 60) определим требуемый коэффициент усиления разомкнутой системы:

1.4. Определение передаточных функций по управляющему,
возмущающему воздействиям и по ошибке.

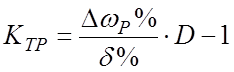
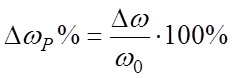
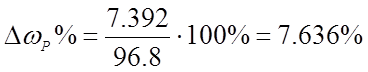
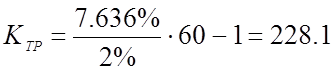
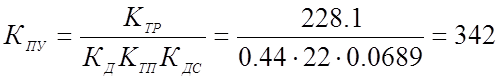
* Передаточная функция разомкнутой системы по управляющему воздействию:

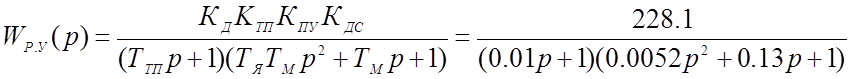
* Передаточная функция замкнутой системы по управляющему воздействию:

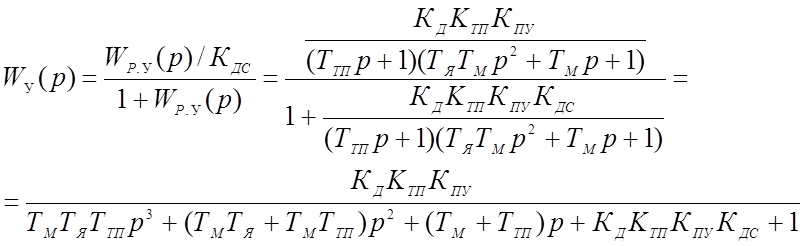
Подставив значения коэффициентов, получим:

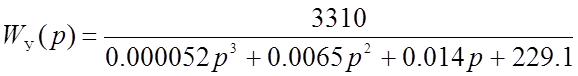
* Передаточная функция разомкнутой системы по возмущению:

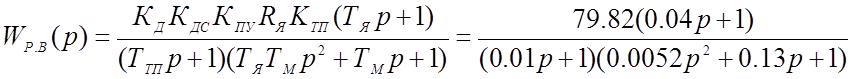
          * Передаточная функция замкнутой системы по возмущению:

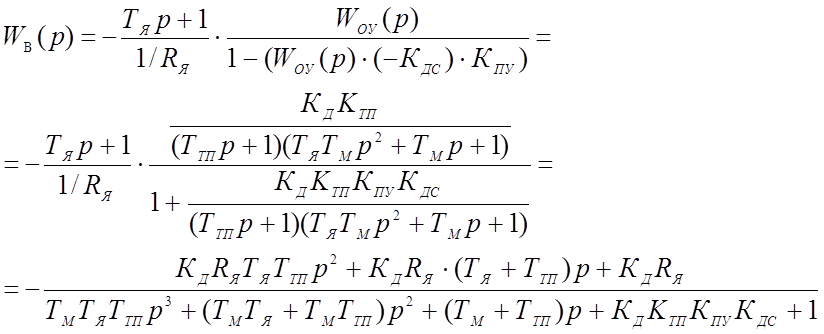
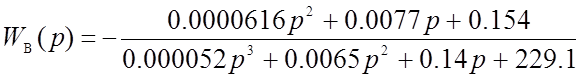
* Передаточная функция по ошибке от управляющего воздействия:

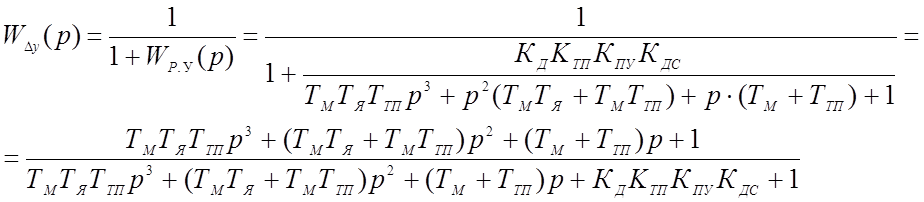
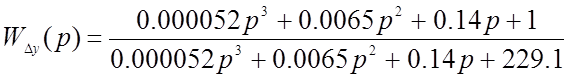
          * Передаточная функция по ошибке от возмущающего воздействия:

1.5. Выводы по проведённому анализу.

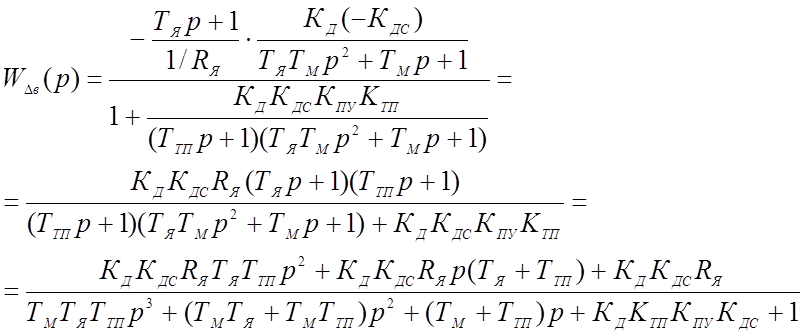
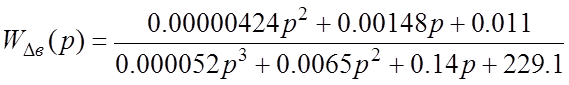
          По полученным в предыдущем пункте передаточным функциям можно сделать следующие выводы:

– знаменатели передаточных функций разомкнутых систем по управляющему и возмущающему воздействию равны;

– знаменатели передаточных функций замкнутых систем по управляющему и возмущающему воздействию, а так же знаменатели передаточных функций ошибки от управляющего и возмущающего воздействия, равны;

          Исходная система является статической как по управляющему, так и по возмущающему воздействию, так как в передаточных функциях разомкнутой системы по управляющему и по возмущающему воздействию отсутствует звено чистого интегрирования.

          По передаточной функции ошибки от управляющего воздействия вычислим статическую ошибку системы:

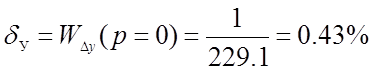, что меньше заданного значения .

2. Анализ устойчивости САУ.

2.1. Анализ устойчивости замкнутой САУ
с помощью алгебраического критерия.

Воспользуемся алгебраическим критерием Рауса.

Характеристический полином получим из передаточной функции замкнутой системы по управляющему воздействию:

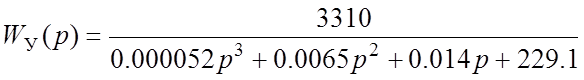
Характеристический полином:

          По данному уравнению строим таблицу Рауса:

Таблица 2.1.1 – Таблица Рауса.

          По условию критерия Рауса система устойчива, если положительны все коэффициенты первого столбца таблицы. По таблице 2.1.1 видно, что рассматриваемая система неустойчива, так как имеет отрицательный элемент в первом столбце.

2.2. Анализ устойчивости с использованием
частотного критерия.

Воспользуемся частотным критерием устойчивости Найквиста. Для использования данного критерия необходимо знать передаточную функцию разомкнутой системы по управляющему воздействию:

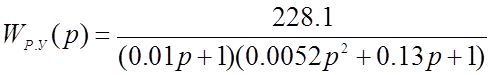
          По критерию Найквиста, система устойчива, если годограф не охватывает точку  (-1; j0). По рисунку 2.2.2 видно, что данная система неустойчива.

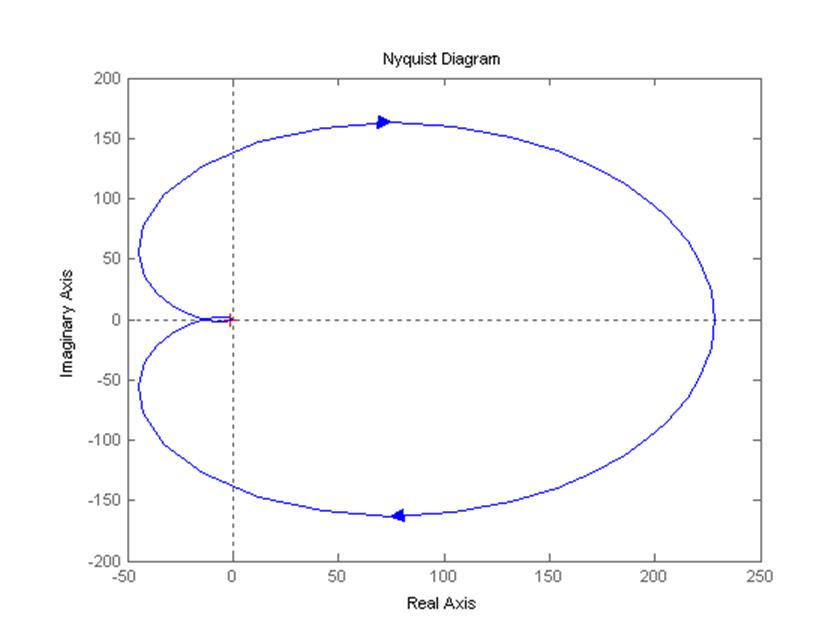
Рисунок 2.2.1 – Годограф Найквиста (общий вид годографа).

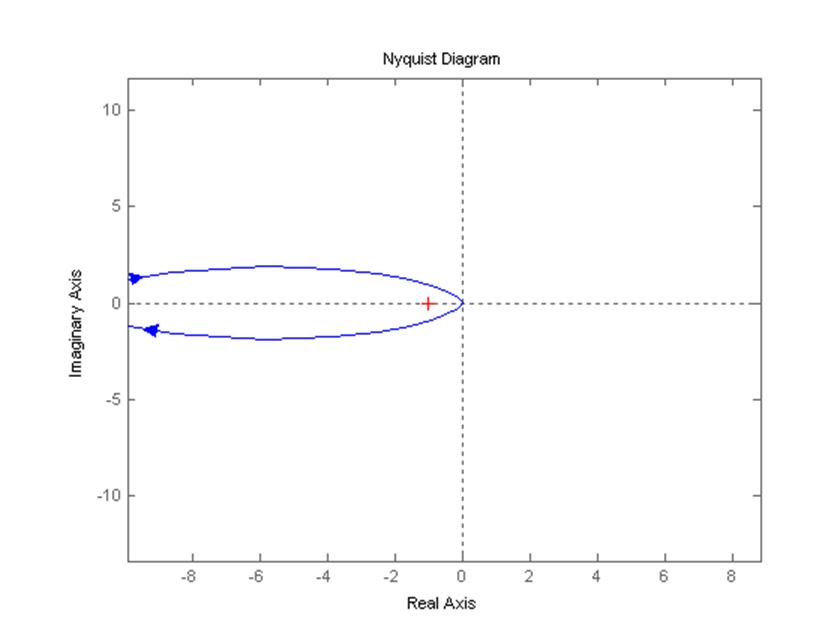
Рисунок 2.2.2. – Годограф Найквиста (вид годографа вблизи точки (-1; j0)).

2.3. Анализ влияния коэффициента усиления
разомкнутой САУ на устойчивость.

          Для анализа влияния коэффициента усиления разомкнутой системы на устойчивость построим корневой годограф.

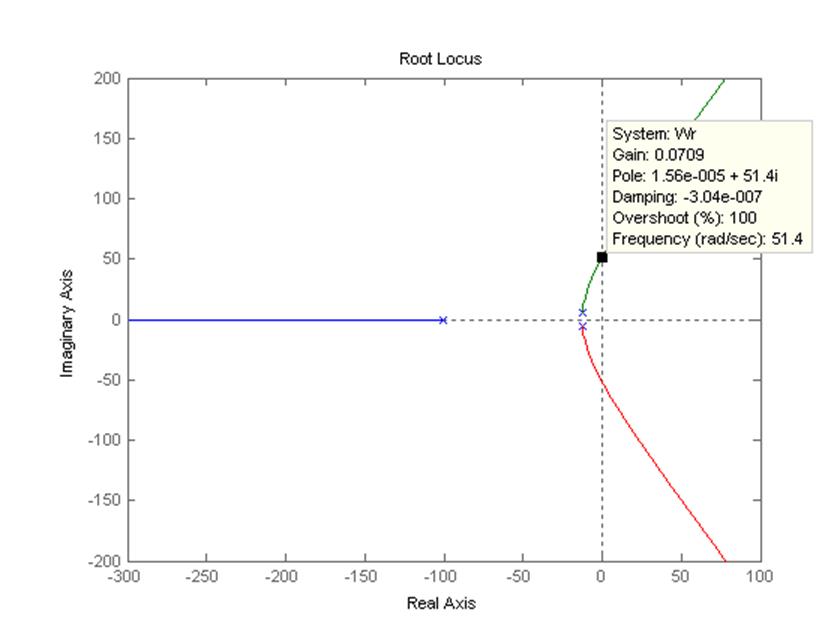
Рисунок 2.3.1 – Корневой годограф.