Теория линейных колебаний. Свободные колебания, страница 3

            Строго говоря (11) является комплексной функцией. Очевидно, что физический смысл имеет, например, линейная комбинация - реальная часть (11):

                                 (12)

В последней функции  начальная амплитуда и фаза определяются из начальных условий.

            Решение (12) представляет собой затухающие колебания . В случае достаточно малого затухания, при  корень в формулах (11), (12) вещественен и приведенные решения описывают затухающий периодический процесс с частотой  и «коэффициентом» затухания - характерным временем затухания колебаний.

            Введем декремент затухания  . Определим его как логарифм отношения соседних амплитуд, отделенных периодом.

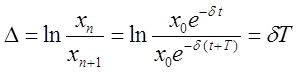                     (13)

Обсудим физический смысл декремента затухания. Для простоты будем считать затухание малым, т.е. изменение амплитуды за период существенно меньше амплитуды: . Подсчитаем потери энергии осциллятора за период. Поскольку диссипация происходит в результате работы силы трения, то:

,

или:

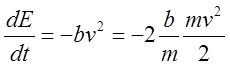.                    (14)

Предполагая затухание малым, можно с хорошей точностью приравнивать кинетическую энергию, согласно теореме вириала половине полной энергии:

.

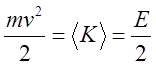Подставляя в (14) получаем уравнение:

 ,

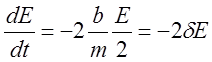решение которого записывается:

.

Учитывая, что энергия пропорциональна квадрату амплитуды, приходим к ранее полученному решению. Итак, энергия осциллятора убывает по экспоненциальному закону. В показателе экспоненты – двойной декремент затухания.

            Введем добротность осциллятора . Определим  следующим образом:

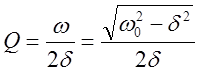                          (15)

В случае малого затухания  . Поскольку  при , то .

Вынужденные колебания.

            Приведем некоторые сведения из алгебры комплексных чисел.

Любое гармоническое решение вида может быть представлено как проекция на ось , вращающегося с угловой скоростью  вектора длины . Соответственно - суть проекция на ось  того – же вектора.

Любое комплексное число может быть представлено в виде:

.

Применительно к гармоническим колебаниям , где соответственно реальная и мнимая части комплексного числа . При перемножении двух комплексных чисел , : - модули перемножаются, а фазы складываются. Для нахождения модуля комплексного числа требуется перемножить число на его сопряженное - : .

            Рассмотрим осциллятор, на который действует гармоническая сила. Будем представлять силу в комплексном виде: . Уравнение колебаний с учетом вынуждающей силы будет записываться в следующем виде:

.

Поделив все на и сгруппировав имеем:

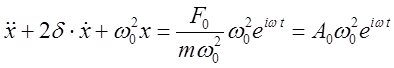                             (16)

Здесь принято обозначение . Решение (16) будем искать в виде:

                                      (17)

   является комплексной амплитудой. После подстановки  в (16) и сокращения экспоненты получаем характеристическое уравнение:

                 (18)

Выражая из последнего , находим зависимость амплитуды колебаний от амплитуды вынуждающей силы:

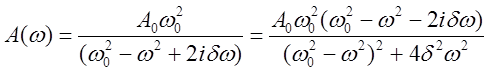             (19)

Очевидно, что  - величина комплексная. Физический смысл имеет ее модуль:

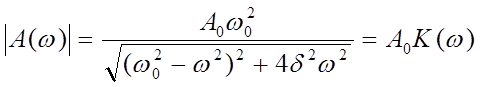                          (20)

- называется коэффициентом передачи системы, или ее амплитудно – частотной характеристикой. График  приведен на рис.n7.

Исследуем свойства .

1. В пределе низких частот, при  коэффициент передачи . При нулевой частоте вынуждающая сила определяет постоянное дополнительное смещение из положения равновесия.