Лекция 9.
Теория линейных колебаний.
Свободные колебания.
Колебаниями называется
периодический процесс. Гармоническими колебаниями называется периодический
процесс с постоянным периодом ![]() . Число периодов
колебаний, происходящих за единицу времени называется частотой колебаний
. Число периодов
колебаний, происходящих за единицу времени называется частотой колебаний ![]() . Введем понятие круговой частоты
. Введем понятие круговой частоты ![]() . Круговая частота и период связаны, как
нетрудно видеть, соотношением
. Круговая частота и период связаны, как
нетрудно видеть, соотношением ![]() . Размерности круговой
частоты
. Размерности круговой
частоты ![]() и частоты
и частоты ![]() совпадают
и равны
совпадают
и равны ![]() - обратному времени.
- обратному времени.
Рассмотрим простую модель осциллятора – модели физического процесса, описываемого уравнениями колебаний. В качестве таковой в дальнейшем исследуется движение точечной массы, привязанной к идеальной пружине. Сила действующая на массу меняется пропорционально удлинению пружины. Такого вида силы вызывают линейные колебания. Строго говоря, модель линейных колебаний справедлива при небольших, в сравнении с характерными размерами физической системы, деформациях. С ростом деформаций относительно положения равновесия в разложении силы могут возникнуть члены пропорциональные квадрату, кубу… смещения. Такие колебания уже не будут называться линейными. Хотя они, возможно, будут описываться периодическими функциями, но их свойства будут отличны от линейных решений.
Уравнение линейных колебаний.
Считая, что сила, действующая на
частицу, пропорциональна смещению ![]() и направлена
противоположно смещению, в положение равновесия
и направлена
противоположно смещению, в положение равновесия ![]() .
Рассматривая одномерное движение запишем уравнение II-го
закона Ньютона:
.
Рассматривая одномерное движение запишем уравнение II-го
закона Ньютона: ![]() , или, вводя параметр
, или, вводя параметр ![]() , имеем:
, имеем:
![]() (1)
(1)
Уравнение (1) называется уравнением свободных, линейных
колебаний. Решение такого уравнения ищется в классе периодических,
гармонических функций ![]() . После подстановки в уравнение
функций вида:
. После подстановки в уравнение
функций вида: ![]() а также линейных комбинаций таких
функций, получаем, что общим решением уравнения (1) является выражение вида:
а также линейных комбинаций таких
функций, получаем, что общим решением уравнения (1) является выражение вида:
![]() , (2)
, (2)
где ![]() , определяются из
начальных данных. Как известно, точное решение дифференциального уравнения
второго порядка требует задания двух значений
, определяются из
начальных данных. Как известно, точное решение дифференциального уравнения
второго порядка требует задания двух значений ![]() и
и ![]() - значения координаты и скорости в
начальный момент времени. Подстановка
- значения координаты и скорости в
начальный момент времени. Подстановка ![]() в
решение (2) позволяет определить для константы
в
решение (2) позволяет определить для константы ![]() .
Действительно:
.
Действительно:
![]() . (3)
. (3)
Пример.
Рассмотрим простые
случаи. Пусть решение имеет вид: ![]() . В этом случае
. В этом случае ![]()
![]()
Графики смещения ![]() , скорости
, скорости ![]() , ускорения
, ускорения ![]() приведены
на рис. n1
приведены
на рис. n1
Энергия осциллятора в отсутствии диссипации является величиной постоянной:
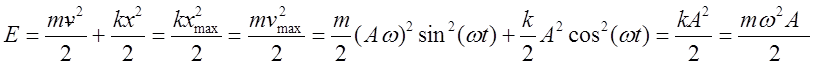 .
.
Последние равенства получены с учетом ![]() . Графики кинетической и потенциальной энергий
как функции времени представлены на рис. n2. Из
графиков видно, что кинетическая энергия меняется в пределах от
. Графики кинетической и потенциальной энергий
как функции времени представлены на рис. n2. Из
графиков видно, что кинетическая энергия меняется в пределах от ![]() до
до ![]() .
Среднее значение кинетической энергии
.
Среднее значение кинетической энергии ![]() .
Аналогично, среднее значение потенциальной энергии
.
Аналогично, среднее значение потенциальной энергии ![]() .
.
![]() (4)
(4)
Видно, что среднее значение кинетической энергии осциллятора равно среднему значению потенциальной энергии. Приведенное утверждение носит название теоремы вириала.
Подстановка средних значений в закон сохранения энергии позволяет получить:
![]() .
.
Замечание. «Осреднение» функций выполняется по времени. Применена теорема о среднем значении функции из анализа. Обыденный смысл процедуры осреднения состоит в срезании бугров функций и заполнении впадин. По волнообразной функции проходит бульдозер. Напомним каноническую формулировку теоремы о среднем значении функции:
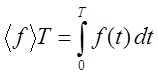
Осреднение кинетической и потенциальной энергий осциллятора
выполняется просто, поскольку функции ![]() обладают
очевидной симметрией.
обладают
очевидной симметрией.
В следующих разделах курса процедура осреднения как повремени, так и подругим переменным будет применяться достаточно часто.
Пример 2. получим уравнение колебаний и решение его для
осциллятора – математического маятника. Физическая модель такого осциллятора –
точечная масса, подвешенная на невесомой, нерастяжимой нити в однородном поле
тяжести (см. рис. n3). При отклонении массы из
вертикального положения равновесия на некоторый угол ![]() возникает
момент силы тяжести, возвращающий массу в положение равновесия
возникает
момент силы тяжести, возвращающий массу в положение равновесия ![]() . Отсчет угла производится относительно
вертикального направления. Момент инерции частицы относительно точки подвеса:
. Отсчет угла производится относительно
вертикального направления. Момент инерции частицы относительно точки подвеса: ![]() , где
, где ![]() - длина
нити. Момент силы:
- длина
нити. Момент силы: ![]() . Запишем основное уравнение
динами вращательного движения твердого тела:
. Запишем основное уравнение
динами вращательного движения твердого тела: ![]() ,
которое применительно к поставленной задаче перепишется:
,
которое применительно к поставленной задаче перепишется:
![]() . Знак – возникает в силу того,
что при выбранном направлении отклонения из положения равновесия момент силы
тяжести вращает частицу по часовой стрелке, направлен перпендикулярно плоскости
рисунка «от нас», в то время как положительными считаются вектора, вращающие
против часовой стрелки – «на нас». После упрощения:
. Знак – возникает в силу того,
что при выбранном направлении отклонения из положения равновесия момент силы
тяжести вращает частицу по часовой стрелке, направлен перпендикулярно плоскости
рисунка «от нас», в то время как положительными считаются вектора, вращающие
против часовой стрелки – «на нас». После упрощения:
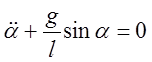 (5)
(5)
Уравнение (5) описывает весь набор возможных колебаний
математического маятника, при произвольных углах отклонения. Колебания будем
называть малыми, если угол отклонения ![]() . В этом
случае в разложении синуса вблизи
. В этом
случае в разложении синуса вблизи ![]() можно пренебречь
членами более высокого порядка по степеням , чем первая. В разложении:
можно пренебречь
членами более высокого порядка по степеням , чем первая. В разложении:
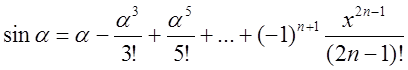 остается
остается ![]() ,
тогда (5) приобретает вид:
,
тогда (5) приобретает вид:
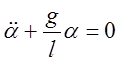 (6)
(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.