Теория линейных колебаний. Свободные колебания, страница 2

Пренебрежение в разложении членами кроме линейного означает другими словами аппроксимацию возвращающей силы линейной функцией, или представлением потенциальной энергии как квадратичной функцией аргумента. .

Фазовая траектория.

Построим эволюцию отображающей точки осциллятора в плоскости координата , скорость . Закон сохранения энергии определяет соотношение между мгновенными значениями потенциальной и кинетической энергий. 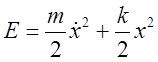. После приведения этого уравнения к каноническому виду убеждаемся, что оно представляет собой уравнение эллипса в плоскости  с полуосями , . Плоскость  называется фазовой, траектория изображающей точки называется фазовой траекторией осциллятора. В случае финитного движения осциллирующей частицы фазовая траектория ограничена.

Задача нахождения периода колебаний.

            Рассмотрим одномерный осциллятор движение которого описывается обощенной координатой  и обобщенной скоростью . В общем случае зависимость потенциальной энергии осциллятора в линейном приближении может быть представлена как:

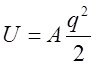. Кинетическая энергия, очевидно: 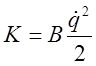. В этих выражениях  некоторые константы, зависящие от геометрии и характеристик движения рассматриваемой физической системы. Утверждается, по аналогии с линейным одномерным осциллятором, что частота колебаний системы определяется из соотношения:

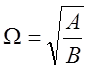.                                (7)

Действительно для линейного осциллятора – грузика на пружинке , и частота колебаний, как было показано ранее . Те – же соображения приводят к (7).

Другой подход. Рассмотрим силы и определим ускорение осциллирующей системы. Очевидно, что результирующая сила может быть представлена как некоторый коэффициент, умноженный на малое приращение обобщенной координаты - . Малое приращение координаты отсчитывается относительно положения равновесия. По второму закону Ньютона найденную силу следует приравнять к обобщённому ускорению, умноженному на эффективную массу осциллятора  . Эффективная масса определяется с учетом геометрии и кинематических связей системы. После определения  коэффициентов при смещении и при ускорении нахождение частоты сводится к вычислению корня из отношения: коэффициент при обобщенном смещении / коэффициент при обобщенном ускорении .

Затухающие колебания.

            Рассмотрим движение осциллятора с потерями энергии. Будем считать, что сила трения, действующая на осциллятор пропорциональна скорости. Уравнение движения в этом случае записывается в виде:

,

где .  - константа. Сила трения противоположно скорости, поэтому стоит отрицательный знак. Рассматривая одномерное движение, где  - смещение из положения равновесия и  окончательно записываем уравнение движения:

                          (8)

Здесь , .  - собственная частота осциллятора. Будем искать решение уравнения в виде: . Дифференцируя его дважды и подставляя в исходное уравнение (8) получаем характеристическое уравнение для определения  - частоты колебаний, при которой существует решение (8):

                           (9)

(9) имеет корни:

                          (10)

Общее решение после подстановки (10) принимает вид:

                      (11)

В (11) выполнена суперпозиция двух решений, соответствующих  соответственно. Константы , как было показано ранее, определяются начальными условиями – значениями координаты и скорости в начальный момент времени.