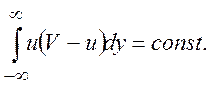Стационарный пограничный слой на пластине в газовом потоке, страница 6

                                          (9.3)

Для того чтобы выяснить физический смысл константы (9.3), применим теорему импульсов к прямоугольной области (L, ± h). На рис. 21 изображена ее верхняя половина. Проекция импульса на ось 0x дает

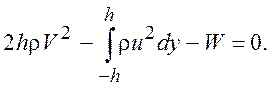                                  (9.4)

Первый член равенства (9.4) определяет импульс на левой границе, а второй – на правой. Здесь W - лобовое сопротивление тела (потеря импульса за счет трения).

Уравнение постоянства расхода запишем в виде

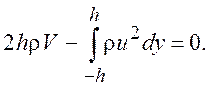                                          (9.5)

Умножив (9.5) на V и вычтя из (9.4), получим, что 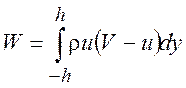 или при y ® ¥:

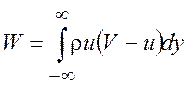.                                             (9.6)

Мы видим, что вдали от тела сохраняет свою величину интеграл (9.3), а из (9.6) следует, что этот интеграл равен лобовому сопротивлению тела.

Можно считать, что на большом удалении от тела величина u’ = V - u мала. Подставим ее в уравнение (9.1), граничные условия (9.2), условие (9.6) и проведем линеаризацию

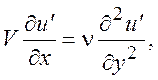                                                  (9.7)

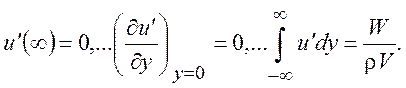                         (9.8)

Введем автомодельную координату

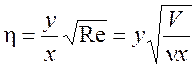.                                                  (9.9)

Решение системы (9.7) с граничными  условиями (9.8) будем искать в виде

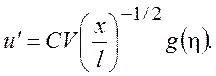                                          (9.10)

Выбор решения в виде (9.10) надо признать удачным потому, что подстановка в (9.6) дает выражение

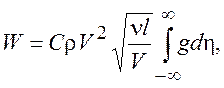                                        (9.11)

которое не зависит от x, т.е. наш “ закон сохранения “ выполняется.

Подставив значение (9.10) в уравнение (9.7), мы получим обыкновенное дифференциальное уравнение

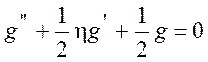                                           (9.12)

с граничными условиями

g’(0) = 0,    g(¥) = 0.                                                (9.13)

Интегрирование уравнения (9.12) дает

                                                  

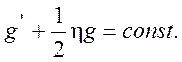
Из первого граничного условия (9.13) получим, что const = 0. Второе интегрирование дает

                                              (9.14)

Определим постоянную A из условия (9.11). Так как

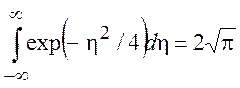
то 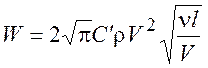                                            ,                                                    (9.15)

здесь C’ = CA = const.

Из решения задачи Блазиуса знаем, что

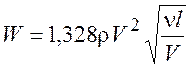.                                            (9.16)

Тогда решение задачи можно представить в окончательном виде

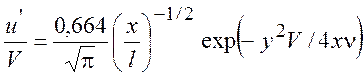.                              (9.17)

По форме решение (9.17) совпадает с кривой Гаусса. Сравнение с экспериментом показало, что решение (9.17) справедливо для x/L > 3.

Отметим, что рассмотренная задача о ламинарном спутном течении не имеет большого практического значения. Полученное решение справедливо на больших расстояниях от тела, но течение в следе неустойчиво и достаточно быстро переходит в турбулентное состояние.

10  ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ

Для большинства задач о движении вязкой жидкости в заданных стационарных условиях должно, в принципе, существовать точное стационарное решение уравнений гидродинамики. Эти решения формально существуют при любых числах Рейнольдса. Но не всякое решение уравнений движения, даже если оно является точным, может реально воплотиться в природе. Движения должны не только удовлетворять гидродинамическим уравнениям, но еще должны быть устойчивыми: малые возмущения, раз возникнув, должны затухать со временем или в пространстве. Если же, напротив, неизбежно возникающие в потоке жидкости сколь угодно малые возмущения стремятся возрасти, то движение неустойчиво и фактически существовать не может.

Математическое исследование устойчивости движения происходит по следующей схеме. На исследуемое стационарное решение (распределение скоростей, в котором пусть будет V₀(x_i) и давление р₀(x_i)) накладывается малое нестационарное возмущение скорости v₁(x_i, t), и давления р₁(x_i, t), которое должно быть определено таким образом, чтобы результирующее движение V=V₀+v₁; р=р₀+р₁, удовлетворяло уравнениям движения, начальным и граничным условиям. Уравнение для определения v₁ и р₁ получается подстановкой их в уравнения движения жидкости, причем считается, что известные функции V₀ и р₀ удовлетворяют стационарным уравнениям.