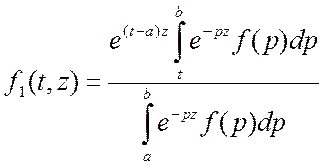
– это целая функция =>
фиксир. t и разлаг.в строку Тейлора по z. Затем вместо z ставим A. Подставим в W(t)
вместо t ![]() a => пропадает вторая скобка, т.к.
a => пропадает вторая скобка, т.к. ![]() .
Первая скобка: интегралы сократятся, а
.
Первая скобка: интегралы сократятся, а ![]() единичная
матрица => E
единичная
матрица => E![]() Wa
Wa
Если t
= b => первая скобка = 0, во второй скобке интегралы
сократятся, а останется Е ![]() Wb,
т.е.совпало.
Wb,
т.е.совпало.
Теперь покажем, что
удовлетворяет ур-ю ![]()
Диф-ем, считая, что А = const
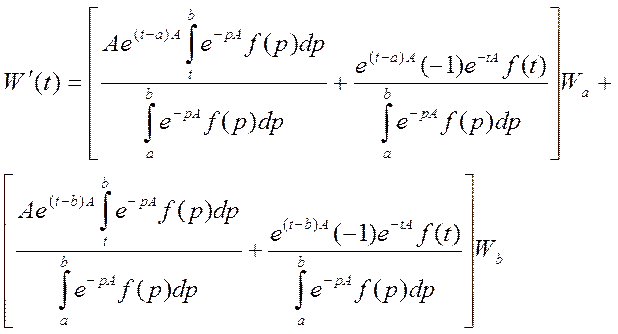
=![]()
– если всё аккуратно подставить
![]()
Понятие линейно зависимой и независимой системы ф-ии (с примерами).
Определение: система функций
y1(t), y2(t),…, ym(t), ![]() называется
линейно зависимой на
называется
линейно зависимой на ![]() , если
, если ![]()
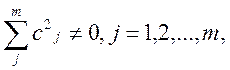 так что
так что 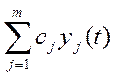 .
Линейно независимы
.
Линейно независимы![]() не удовлетворяет этому условию,
все сj=0.
не удовлетворяет этому условию,
все сj=0.![]() критерий зависимости и независимости:
строится определитель Вронского:
критерий зависимости и независимости:
строится определитель Вронского: 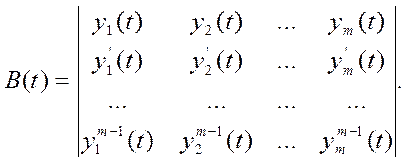
ФСР линейного уравнения n-ного порядка с постоянными коэффициентами
Теорема: пусть ![]() - корни характеристического уравнения
- корни характеристического уравнения ![]() ; (кратность)
; (кратность) ![]() . Тогда
можно построить по каждому корню
. Тогда
можно построить по каждому корню ![]() систему функций
систему функций ![]() эта система есть ФСР
эта система есть ФСР
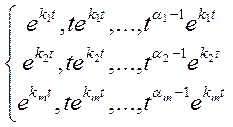 ,
первое уравнение записано по первому корню и т.д.
,
первое уравнение записано по первому корню и т.д.
Таких уравнений n штук и они линейно независимы. Теперь надо решать само уравнение.
Доказательство: рассмотрим
случай, что кратность каждого корня = 1, т.е. ![]() ,
, ![]() - n функций. Надо
показать, что каждая функция является решением и они линейно независимы. Будем
искать решение в виде
- n функций. Надо
показать, что каждая функция является решением и они линейно независимы. Будем
искать решение в виде ![]() дифференцируем n
раз
дифференцируем n
раз ![]()
![]() . Докажем, что они
линейно независимы. Пусть они линейно зависимы
. Докажем, что они
линейно независимы. Пусть они линейно зависимы ![]()
![]() . Пусть, если
. Пусть, если ![]() .
Дифференцируем
.
Дифференцируем ![]()
![]() -
пропадёт! И т.д.
-
пропадёт! И т.д. ![]() вытекает что они линейно
независимы!
вытекает что они линейно
независимы!
Если корень комплексный ![]() существуют сопряженные
существуют сопряженные ![]()
![]() и
и ![]() - тоже решения.
- тоже решения.
Если корни имеют кратность:
пусть первый корень нулевой, т.е. ![]() , его кратность
равняется
, его кратность
равняется ![]()
![]()
![]()
![]() - такой вид уравнения
- такой вид уравнения ![]() решения
решения ![]() (если
подставить). А если
(если
подставить). А если ![]() - тоже решение. Если же корень
ненулевой
- тоже решение. Если же корень
ненулевой ![]() - рассмотрим функцию. Она удовлетворяет
новому уравнению и имеет нулевой корень кратности
- рассмотрим функцию. Она удовлетворяет
новому уравнению и имеет нулевой корень кратности ![]() , а
далее подставим и получим те не решения. Можно иначе: если
, а
далее подставим и получим те не решения. Можно иначе: если ![]() - корень, то и произв. ф-ции имеет корень,
только порядка на единицу меньше.
- корень, то и произв. ф-ции имеет корень,
только порядка на единицу меньше.
Пример: ![]() все производные по k
(19)ой степ. имеют корень 2. Поэтому эти функции являются решениями!
все производные по k
(19)ой степ. имеют корень 2. Поэтому эти функции являются решениями!
Покажем, что они лин. незав.
![]()
По индукции: для 2t
Пусть ![]()
![]() ,
, ![]()
![]()
![]()
![]() . Берем произв. столько
раз, чтобы на единицу больше, чем степень левого полинома
. Берем произв. столько
раз, чтобы на единицу больше, чем степень левого полинома ![]() =0
=0 ![]()
![]()
![]()
![]() противоречие.
И т.д. – по индукции (таким же методом)
противоречие.
И т.д. – по индукции (таким же методом)
Уравнение колебаний
струны. Общее решение ![]()
(1) 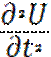 =
= 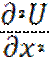 (-∞ < x
< +∞); (t ≥ 0)
(-∞ < x
< +∞); (t ≥ 0)
(1) U|t=0 = U0(x) ![]() |t=0
= U1(x)
|t=0
= U1(x)
(1)&(2) – задача Коши
+ здесь же написать формулу Даламбера.
Система линейных уравнений первого порядка с постоянными коэффициентами на плоскости. типы точек покоя.
Это равносильно характеристике
поведения. 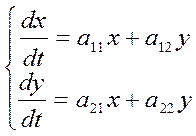 .
. 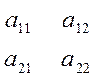 - матрица.
- матрица.
(0;0) – точка покоя, нулевое
решение. Фазовая плоскость – это как ведет себя решение в окрестности точки
покоя. 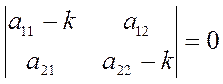 -
характеристическое уравнение.
-
характеристическое уравнение.
(1) 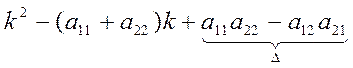 =0
=0
*1) ![]()
![]() - корни уравнения (1).
Так мы получили характеристическое уравнение
- корни уравнения (1).
Так мы получили характеристическое уравнение 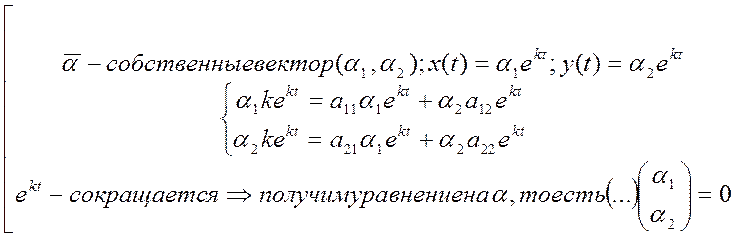 .
.
Решения:![]() , а
, а ![]()
:![]() , а
, а ![]() , где
, где 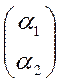 и
и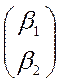 - собственные векторы.
Любое решение линейной комбинации этих двух решений. Займемся теперь поведением
решения в точке покоя:
- собственные векторы.
Любое решение линейной комбинации этих двух решений. Займемся теперь поведением
решения в точке покоя:
1 случай: корни к1
и к2 – различны (к1 и к2![]() решения
уходят на +
решения
уходят на +![]() , растут.(рисунок).
, растут.(рисунок).
2 случай: к1 и к2![]() с ростом t
стремятся решения к нулю.(рисунок)
с ростом t
стремятся решения к нулю.(рисунок)
3 случай: к1>0,
а k2<0![]() «седло» (рисунок)
«седло» (рисунок)
4 случай: комплексные корни
(и к1 и k2) ![]()
![]() По формуле Эйлера
записать, отдельно линейную отдельно мнимую часть.
По формуле Эйлера
записать, отдельно линейную отдельно мнимую часть.
А)p>0 (рисунок)
Б)p<0 (рисунок)
В)p=0 (рисунок)
*Если же корни равны ![]()
![]()
![]()
![]() , если k1<0
, если k1<0![]() устойчивый узел, если k1>0
устойчивый узел, если k1>0![]() неустойчивый
узел.
неустойчивый
узел.
* ![]() Если det=0
Если det=0![]() траектория – прямые линии.
траектория – прямые линии.
Так как один корень =0 (K=0); 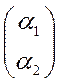 и
и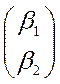 -
собственные вектора.(
-
собственные вектора.(![]() )
)
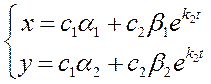 .
. 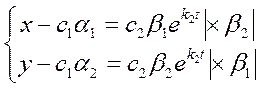 и приравнять.
и приравнять. ![]() уравнение
прямой.
уравнение
прямой. ![]() постоянное решение.
постоянное решение. ![]() устойчивое
решение.
устойчивое
решение.
Пример: ![]() колебание с затуханием. Это линейное
уравнение 2-ого порядка.
колебание с затуханием. Это линейное
уравнение 2-ого порядка.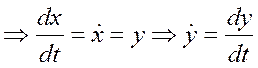
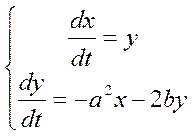
![]() (характеристическое
уравнение.
(характеристическое
уравнение. 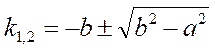
1)b=0![]() «центр», корни комплексные,
сопряженные. Чисто периодическое решение!
«центр», корни комплексные,
сопряженные. Чисто периодическое решение!
2)b>0,
а ![]() устойчивый фокус.
устойчивый фокус.
3) b>0,
а ![]() устойчивый узел.
устойчивый узел.
4) b<0,
а ![]() неустойчивый фокус.
неустойчивый фокус.
5) b<0,
а ![]() неустойчивый узел.
неустойчивый узел.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.