Доказательство: (с использованием теоремы о неподвижной точке).
Вводится пространство М –
непрерывных функций x(t), t![]()
Это полное метрическое
пространство. «Полнота» вытекает из свойств чисел (![]() фундаментальная
последовательность сходится).
фундаментальная
последовательность сходится).
Теперь строим из (1)
оператор: пусть существует некое решение задачи Коши ![]() -
непрерывна
-
непрерывна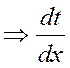 - непрерывна
- непрерывна![]() интегрируется
от t до tfix
интегрируется
от t до tfix ![]()
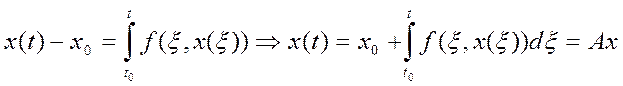 -
оператор.
-
оператор.
Ax= 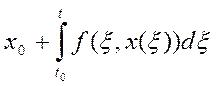 Каждой неопределенной функции оператор
ставит в соответствие другую неопределенную функцию. Если x(t) – решение (1)
Каждой неопределенной функции оператор
ставит в соответствие другую неопределенную функцию. Если x(t) – решение (1)![]() x(t) – неподвижная точка, так как x(t)=Ax.
x(t) – неподвижная точка, так как x(t)=Ax.
Обратно: пусть x(t) – неподвижная точка, при ![]()
![]() получаем
задачу Коши – выполняется система. Функция
получаем
задачу Коши – выполняется система. Функция ![]() -
дифференцируема, так как суперпозиция непрерывных функций, и вместо
-
дифференцируема, так как суперпозиция непрерывных функций, и вместо ![]() Следовательно, для того чтобы
Следовательно, для того чтобы ![]() - было решением задачи Коши, необходимо и
достаточно, чтобы
- было решением задачи Коши, необходимо и
достаточно, чтобы ![]() - была неподвижной точкой такого
оператора Ах, то есть проведена редукция. Теперь надо понять, когда же оператор
будет сжимающим?
- была неподвижной точкой такого
оператора Ах, то есть проведена редукция. Теперь надо понять, когда же оператор
будет сжимающим? ![]() . Посчитаем:
. Посчитаем: 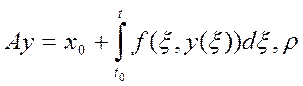 - это sup
- это sup![]() найдем:
найдем: 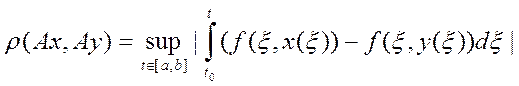 .
.
Рассмотрим 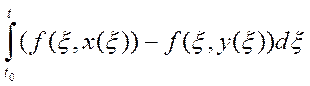
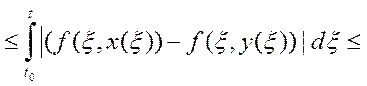
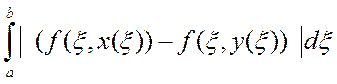 (по
условию Липшица)
(по
условию Липшица)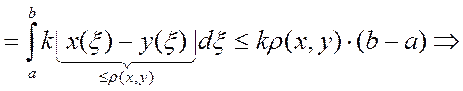 не зависит от t
не зависит от t![]() и sup тоже
не
и sup тоже
не
зависит от t![]()
описываем: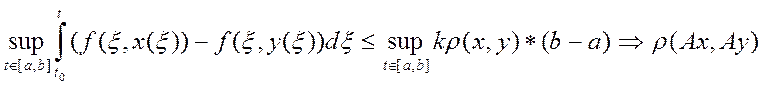 - по определению
- по определению 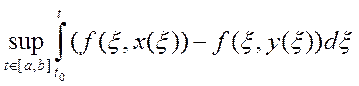
![]()
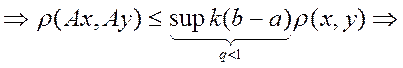 это сжимающее.
Следовательно x(t) –
неподвижная точка и значит задача Коши имеет единственное решение.{Для системы
сформулировать самим n(b-a)k=q<1}.
это сжимающее.
Следовательно x(t) –
неподвижная точка и значит задача Коши имеет единственное решение.{Для системы
сформулировать самим n(b-a)k=q<1}.
Пример: (решение имеется, но не единственное)
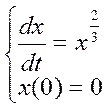 ,
условие Липшица не выполняется.
,
условие Липшица не выполняется.
Здесь как min
2 решения: x = 0 и x(t) = 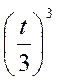 .
. 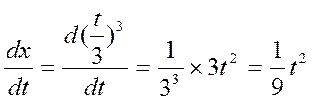 .
. 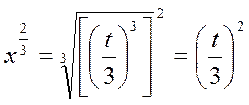
Задача Дирихле для уравнения Лапласа.
Задача:
Восстановить гармоническую функцию ![]() в обл D по значениям на границе
в обл D по значениям на границе ![]()
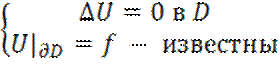 уравнение Дирихле для уравнения Лапласа
уравнение Дирихле для уравнения Лапласа
Задача
Дирихле для уравнения Лапласа имеет не более одного решения из ![]() .
.
Док-во:
пусть ![]() 2 решения
2 решения ![]() и
и ![]()
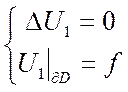 и
и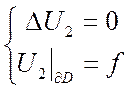
Введем
функцию V=![]() =>
=>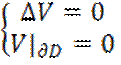 => и min, и max=0 (т.к. дост на границе)=> по принципу max V=0 =>
=> и min, и max=0 (т.к. дост на границе)=> по принципу max V=0 =>
![]() =
=![]() ч.т.д.
ч.т.д.
Теорема о единственности для гармонической функции. (без свойств гармонической функции)
Th1: Гармоничная ф-ция класса ![]() однозначно определяется на границе
однозначно определяется на границе ![]() обл D
обл D
Доказательство:
I Для 2-х переем: n=2
U(x,y),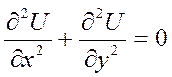 ,
, ![]() Нужно док-ть, что U(x,y)
Нужно док-ть, что U(x,y)![]() 0
0 ![]()
![]()
![]()
1.
Ф-ла
Грина 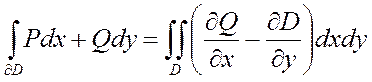
Q
и P ![]()
2.
Полагаем
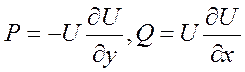 , где U(x,y)- любая ф-ция
класса
, где U(x,y)- любая ф-ция
класса![]()
Тогда 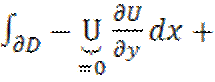
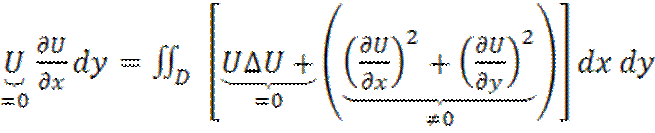
3.
Возьмем
в кач-ве ее U – гармонич
=>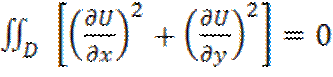
4.
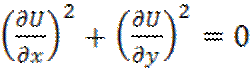 (x,y)
(x,y)![]() =>
=>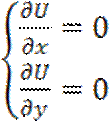 (x,y)
(x,y)![]()
5.
Т.к.
![]() непр ч.п.,
которая = 0 => U=const
непр ч.п.,
которая = 0 => U=const
6.
Т.к.
![]()
![]() =>
U(x,y)=0 (c=0) ч.т.д.
=>
U(x,y)=0 (c=0) ч.т.д.
II n=3 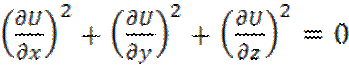 ,
, ![]()
1.
Гаусса-
Остраградского 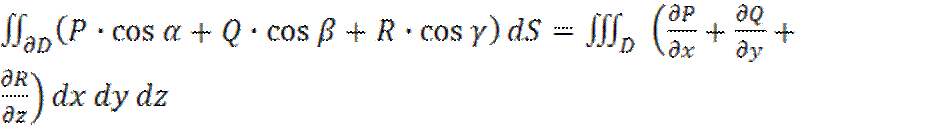
2.
P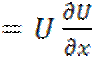 ; Q
; Q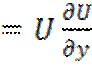 ; R
; R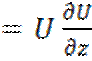 , где
, где ![]() произволная
ф-ция класса
произволная
ф-ция класса ![]() =>
=>
3.
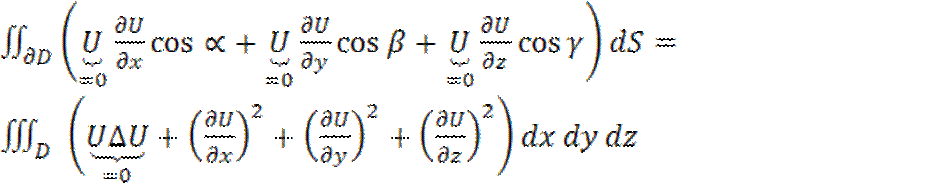 Возьмем в кач-ве U:
Возьмем в кач-ве U: ![]() и
и ![]() =>
=> 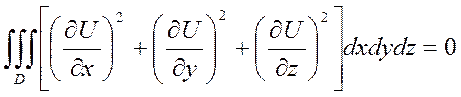
4.
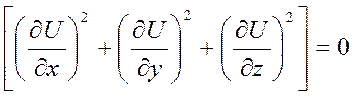 т.к. инт-л равен 0 =>
т.к. инт-л равен 0 =>
![]()
![]()
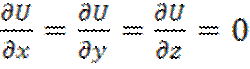
5. Т.к.
U имеет ч.п.=0
=> ![]() =const
=const ![]() (x,y,z)
(x,y,z) ![]()
5.
Т.к.
![]() => const=0 =>
=> const=0 => ![]() =0 в D, ч.т.д.
=0 в D, ч.т.д.
Определение понятия устойчивости и асимптотической устойчивости по Ляпунову.
Элементы теории устойчивости
(1)
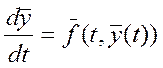 - n
штук функций
- n
штук функций ![]() - непрерывно
дифферинциируемая функция
- непрерывно
дифферинциируемая функция
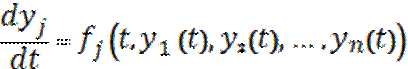 , j=1,2,…,n
, j=1,2,…,n
По решению задачи Коши ![]() решение, устойчивое для малых t, т.е. мало меняется в окрестности
решение, устойчивое для малых t, т.е. мало меняется в окрестности ![]() {из теории неподвижных точек}.
Локальная устойчивость вытекает из теоремы неподвижных точек. Ляпунов ввел
понятие устойчивости!
{из теории неподвижных точек}.
Локальная устойчивость вытекает из теоремы неподвижных точек. Ляпунов ввел
понятие устойчивости!
Определение: Решение ![]() системы уравнений (1)
называется устойчивым по Ляпунову, если для любого
системы уравнений (1)
называется устойчивым по Ляпунову, если для любого ![]() , такая что
, такая что ![]() - решение (1):
- решение (1):
![]()
![]()
![]() устойчивость
в случае центра, устойчивость в случае узла и устойчивость в случае фокуса.
устойчивость
в случае центра, устойчивость в случае узла и устойчивость в случае фокуса.
Если при этом выполнено
условие: ![]() асимптотически устойчива
асимптотически устойчива
Понятие о ФСР линейных уравнений.
Рассмотрим: ![]() aj(t) – непрерывны на
aj(t) – непрерывны на ![]() . Если f(t)=0
. Если f(t)=0 ![]() однородное уравнение. Если aj(t) = const
однородное уравнение. Если aj(t) = const ![]() линейное уравнение с постоянными
коэффициентами. Задача Коши для этого уравнения: уравнение +
линейное уравнение с постоянными
коэффициентами. Задача Коши для этого уравнения: уравнение + ![]() , k=1,2,…,n-1,
, k=1,2,…,n-1, ![]() . Здесь тоже есть общее
и частное решение. Имеет место фундаментальный факт: уравнение имеет ровно n линейно независимых решений
. Здесь тоже есть общее
и частное решение. Имеет место фундаментальный факт: уравнение имеет ровно n линейно независимых решений![]() система
из n уравнений – фундаментальная система решений
и все остальные выражаются линейно через неё.
система
из n уравнений – фундаментальная система решений
и все остальные выражаются линейно через неё.
EX: y’’+a2y=0![]() решения sin(at) и cos(at). y(t)= c1cos(at)+c2sin(at) – это
решения sin(at) и cos(at). y(t)= c1cos(at)+c2sin(at) – это
![]() решение.
решение.
Метод разделения переменных и его использование при решении начальных краевых задач ( Метод Фурье) – уравнение теплопроводности, волновое уравнение.
1 - Ур-е теплопроводности:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.