Швидкість
збіжності квадратурної формули визначається оцінкою залишкового члена. Тобто,
якщо ![]() , то квадратурна формула називається
збіжною з р – порядком збіжності (нагадаємо, що для формули середніх,
формули трапеції р=2, а для формули парабол р=4). Як правило,
підінтегральна функція при цьому повинна мати похідну, яка входить до
залишкового члена. Доведено, що чисельне інтегрування стійке за вхідними
даними, хоча квадратурні формули нестійкі відносно похибок округлення, але ця
нестійкість слабка і виявляється лише за розрахунків з малою кількістю
правильних цифр.
, то квадратурна формула називається
збіжною з р – порядком збіжності (нагадаємо, що для формули середніх,
формули трапеції р=2, а для формули парабол р=4). Як правило,
підінтегральна функція при цьому повинна мати похідну, яка входить до
залишкового члена. Доведено, що чисельне інтегрування стійке за вхідними
даними, хоча квадратурні формули нестійкі відносно похибок округлення, але ця
нестійкість слабка і виявляється лише за розрахунків з малою кількістю
правильних цифр.
Приклад. Обчислення
інтеграла 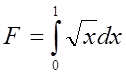 . У підінтегральної функції
перша похідна необмежена, тому використаємо метод Ейткена для оцінки похибки.
Ефективний порядок точності невідомий. Складемо таблицю значень функції й
обчислимо інтеграл за формулами трапецій і Симпсона при різних кроках.
. У підінтегральної функції
перша похідна необмежена, тому використаємо метод Ейткена для оцінки похибки.
Ефективний порядок точності невідомий. Складемо таблицю значень функції й
обчислимо інтеграл за формулами трапецій і Симпсона при різних кроках.
|
х |
|
|
Трапецій |
Симпсона |
Ейткена |
|
0,00 0,25 0,50 0,75 1,00 |
0,0000 0,5000 0,7071 0,8660 1,0000 |
1,00 0,50 0,25 |
0,5000 0,6036 0,6433 |
–0,6381 0,6565 |
– – 0,6446 |
Як
бачимо, дві формули дають результати невисокої точності. Погана точність
формули Симпсона означає, що формула трапецій має фактично не другий порядок
точності й уточнення методом Рунге тут недоцільне. А уточнення першого стовпця
таблиці процесом Ейткена значно покращує результат; водночас з’ясовується, що в
даному прикладі ефективний порядок точності формули трапецій ![]() .
.
Ефективний порядок точності виявився не цілим числом! З цим доводиться стикатися, якщо функція має особливості, а формула інтегрування явно цього не враховує, або якщо особливості має сама формула (це можливо в нелінійних формулах інтегрування).
Якщо
ніяких особливостей немає, то ефективний порядок точності може лише трішки
відрізнятися від теоретичного завдяки наявності у похибці не лише головного
члена, але й членів більш високого порядку малості. У такому випадку при ![]() ефективний порядок прямує до теоретичного.
ефективний порядок прямує до теоретичного.
Для обчислень можна використати пакет Maple:
> F1:=0.5;
![]()
> F2:=0.6036;
![]()
> F3:=0.6433;
![]()
> F:=F1+(F1-F2)^2/(2*F2-F1-F3);
![]()
> q:=0.5;
![]()
> beta=F-F1;
![]()
> p=ln(q)^(-1)*ln((F3-F2)/(F2-F1));
![]() .
.
Отже, якщо необхідно оцінити доцільність використання певної квадратурної формули до безпосередніх розрахунків, то необхідно скористатися апріорними оцінками похибки квадратурних формул, оскільки саме вони дають можливість оцінити точність даної формули, без виконання обчислень. Але, якщо апріорно неможливо оцінити похибку квадратурної формули, або необхідно виконати обчислення і додатково оцінити похибку квадратурної формули, то можна скористатися апостеріорними оцінками квадратурних формул, які дозволяють зробити оцінку похибки безпосередньо під час розрахунків.
Використавши один із методів оцінки похибки квадратурних формул, можна оцінити точність проведення обчислень для поставленого завдання, якщо необхідно – вибрати оптимальний варіант обчислень, тобто найбільш точну формулу для даного випадку.
Розглянемо K-вимірний інтеграл вигляду
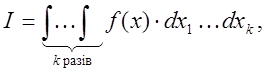 (7.16)
(7.16)
де ![]() - деяка K-вимірна точка. Далі розглянемо
подвійні інтеграли (K=2), оскільки їх можна інтерпретувати графічно.
- деяка K-вимірна точка. Далі розглянемо
подвійні інтеграли (K=2), оскільки їх можна інтерпретувати графічно.
Кубатурні формули, або формули чисельних кубатур, призначені для чисельного визначення кратних інтегралів.
Нехай функція ![]() визначена й неперервна в деякій
обмеженій області
визначена й неперервна в деякій
обмеженій області ![]() . У цій області
. У цій області ![]() вибирається система точок (вузлів)
вибирається система точок (вузлів) ![]() . Для обчислення інтеграла
. Для обчислення інтеграла 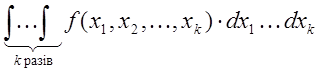 приблизно покладемо
приблизно покладемо
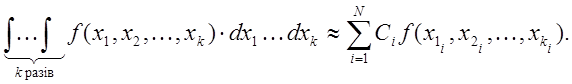 (7.17)
(7.17)
Щоб
знайти коефіцієнти ![]() , зажадаємо точного виконання
кубатурної формули (7.17) для всіх поліномів
, зажадаємо точного виконання
кубатурної формули (7.17) для всіх поліномів
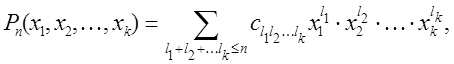 (7.18)
(7.18)
степінь
яких не перевищує заданого числа ![]() . Для цього необхідно й
достатньо, щоб формула (7.17) була точною для добутку степенів
. Для цього необхідно й
достатньо, щоб формула (7.17) була точною для добутку степенів
![]() . Покладаючи в (7.17)
. Покладаючи в (7.17) ![]() , маємо:
, маємо:
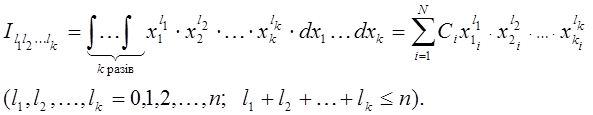 (7.19)
(7.19)
Таким
чином, коефіцієнти ![]() формули (7.17) можуть бути
визначені із системи лінійних рівнянь (7.19).
формули (7.17) можуть бути
визначені із системи лінійних рівнянь (7.19).
Для
того щоб система (7.19) мала розв’язок, необхідно, щоб
число невідомих ![]() дорівнювало числу рівнянь. У
випадку подвійного інтеграла (
дорівнювало числу рівнянь. У
випадку подвійного інтеграла (![]() ) одержуємо
) одержуємо
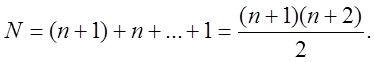
7.6 Вибір кубатурних формул
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.