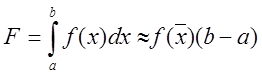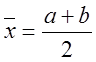Чисельне інтегрування функцій. Квадратурні формули Ньютона-Котеса. Квадратурна формула Гауса, страница 2

  ().

Це найпростіша квадратурна формула. Розклавши  у ряд Тейлора довкола точки   

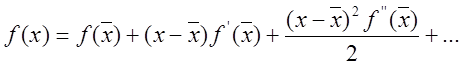
і підставивши цей ряд в інтеграл, одержимо значення похибки формули середніх

.

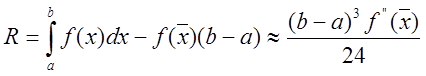Формула середніх є точною для лінійної підінтегральної функції , оскільки тоді .

Природно, що точність формули  для довільної  можна підвищити, якщо скористатися докладнішою сіткою

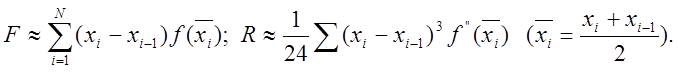Це так звана складена формула середніх або формула прямокутників. У разі рівномірної сітки, тобто якщо ,  формула виглядатиме так:

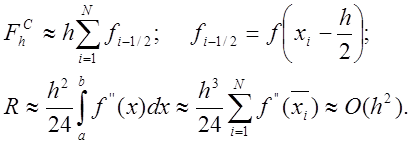
Наведені оцінки R справедливі, якщо існує неперервна ; якщо ж  кусково-неперервна, має місце лише мажорантна оцінка

.

7.1.2 Формула трапецій

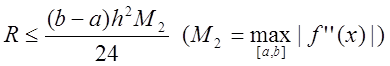Замінимо функцію  на відрізку  інтерполяційним поліномом Лагранжа першого степеня з вузлами , що відповідає заміні кривої  на січну. Тоді значення шуканого інтеграла (площу криволінійної трапеції) можна наближено замінити на площу трапеції з висотою  та основами . Отже, формула трапеції матиме вигляд

.

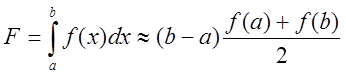Формула трапеції буде точною для лінійної підінтегральної функції з тієї самої причини, що й формула середніх.

На докладнішій сітці  одержимо складену формулу трапецій:

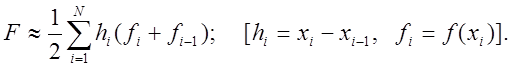
На рівномірній сітці вона стає такою:

).

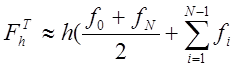Зазначимо, що для одержання залишкового члена формули трапеції потрібно замінити чисельний коефіцієнт (1/24) у залишковому члені формули середніх на (-1/24).

7.1.3 Формула Симпсона

Квадратурна формула Симпсона є частковим випадком квадратурних формул Ньютона-Котеса при . Тут підінтегральна функція заміняється інтерполяційним поліномом Лагранжа 2-го степеня (рисунок 7.2). Із цієї причини формулу Симпсона ще називають формулою парабол.

Розіб’ємо відрізок  на 2 рівних відрізки і одержимо сітку , що містить три вузли. Формула Симпсона містить три коефіцієнти Котеса:

;   .

.

;  .

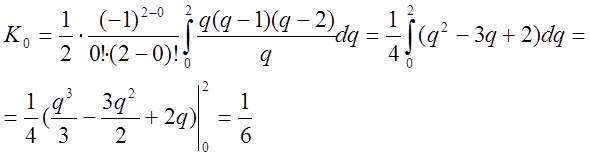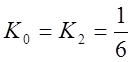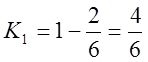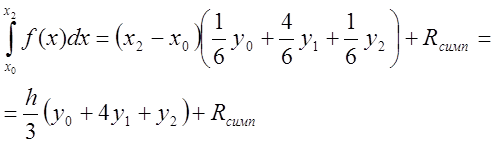         (7.5)

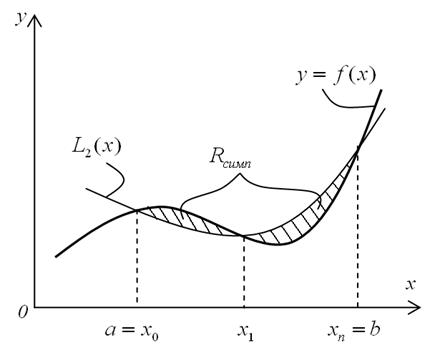
Рис. – 7.2

Формула (7.5) є трьохточковою квадратурною формулою Симпсона.

Якщо  розбити на парну кількість відрізків, що дорівнює , і до кожного часткового здвоєного проміжку ,,…, застосувати формулу Симпсона, то одержимо складену формулу Симпсона

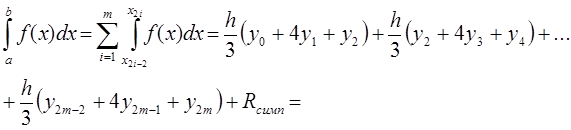
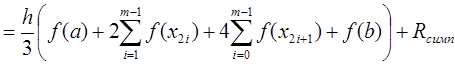.                         (7.6)

Урахувавши, що головні члени похибок у формулі середніх та формулі трапеції одного порядку, але  різних знаків, можна одержати точнішу квадратурну формулу. Для цього скомбінуємо ці формули так, щоб головний член сумарної похибки цих квадратурних формул перетворився на нуль, тобто

.

Отже, дійдемо формули парабол

.

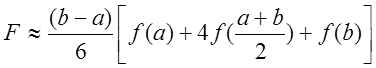Формула парабол є точною для кубічної підінтегральної функції , оскільки в похибку  входитиме , а вона для такої підінтегральної функції дорівнює нулю.

Ця формула має такий залишковий член:

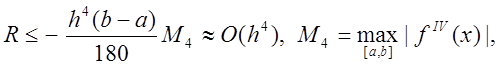
тобто формула парабол має 4-й порядок похибки, а чисельний коефіцієнт досить малий. Через ці обставини формула парабол дає добру точність за відносно невеликого числа вузлів, якщо  не дуже велика.

Приклад реалізації алгоритму чисельного інтегрування функції одного аргумента за формулою Симпсона на псевдокоді

f(x):

   //Повертає значення підінтегральної функції

end

//Повертає одну суму з формули Симпсона

//a – лівий кінець відрізка інтегрування

//h – крок

sum1(n,h,a):

1  temp:=0

2  for i:=1 to (an div 2) do

3   temp+=f(a+(2*k-1)*ah)

4  done

5  return temp

end

//Повертає одну суму з формули Симпсона

//a – лівий кінець відрізка інтегрування

//h – крок

sum2(n,h,a):

1  temp:=0;

2  for k:=2 to (an div 2) do

3   temp+=f(a+(2*k-2)*ah)

4  done

5  return temp

end

Calc_Integrate_Simpson(a,b,

1  n:=4

2  h:=(b-a)/n

3  repeat

4  I1:=(h*(f(a)+f(b)+4*sum1(n,h,a)+2*sum2(n,h,a)))/3;

5   n:=2*n;

6  h:=(b-a)/n;

7  I2:=(h*(f(a)+f(b)+4*sum1(n,h,a)+2*sum2(n,h,a)))/3

8     m:=abs(I1-I2)

9  until (m<eps)

10  returnI2

end

7.2 Квадратурна формула Гауса

Загальний підхід для побудови квадратурної формули для інтегралів 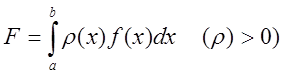 полягає у виборі параметрів фіксоване) так, щоб забезпечити максимально можливий степінь точності. Квадратурна формула з такою властивістю носить назву формули Гауса. У розглянутих квадратурних формулах вибирали і знаходили вузли та ваги, а отже, тим самим не було використано всі можливості загальної квадратурної формули.