К.Ф.Гаус
звернув увагу, що квадратурна формула має ![]() невідомих
параметрів
невідомих
параметрів ![]() та
та ![]() , тобто саме
стільки, скільки параметрів має алгебраїчний поліном степеня
, тобто саме
стільки, скільки параметрів має алгебраїчний поліном степеня ![]() . Він запропонував підбирати ці параметри
так, щоб квадратурна формула була точною для підінтегральної функції
. Він запропонував підбирати ці параметри
так, щоб квадратурна формула була точною для підінтегральної функції ![]() у вигляді полінома степеня, не вищого за
у вигляді полінома степеня, не вищого за ![]() .
.
Спочатку
для спрощення розглянемо відрізок ![]() , тобто інтеграл вигляду
, тобто інтеграл вигляду
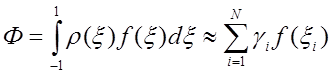 (7.7)
(7.7)
Отже,
знайдемо параметри ![]() з таких умов:
з таких умов:
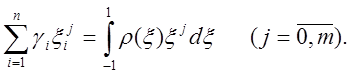 (7.8)
(7.8)
Це
система ![]() нелінійних алгебраїчних рівнянь відносно
нелінійних алгебраїчних рівнянь відносно ![]() ,
, ![]() .
.
Для
подальшого спрощення вважатимемо, що ![]() .
.
Якщо
![]() одержимо
одержимо ![]() і
система
і
система 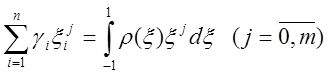 набере вигляду
набере вигляду
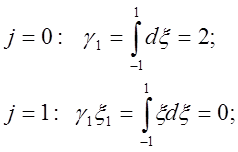
із другого рівняння
випливає, що ![]() , тобто дійшли відомої формули середніх для
відрізка
, тобто дійшли відомої формули середніх для
відрізка ![]()
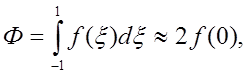
яка є точною для будь-якого полінома 1-го степеня.
Якщо
![]() , система
, система 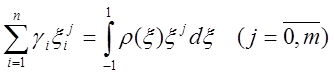 матиме
такий вигляд (
матиме
такий вигляд (![]() ):
):
![]()
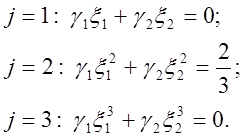
Розв’язавши цю систему, знайдемо:
![]()
тобто маємо квадратурну формулу
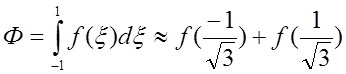 ,
,
яка є точною для будь-якого полінома 3-го степеня.
За
довільного ![]() як вузли квадратурної формули Гауса беруть
нулі поліномів Лежандра
як вузли квадратурної формули Гауса беруть
нулі поліномів Лежандра
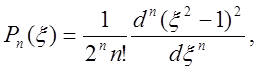
а ваги цієї квадратурної формули визначають за таким виразом:
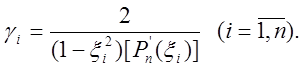 (7.9)
(7.9)
Маючи
значення ![]() та вузлів
та вузлів ![]() на
відрізку
на
відрізку ![]() , значення інтеграла на довільному відрізку
, значення інтеграла на довільному відрізку
![]() обчислюється за такою квадратурною
формулою Гауса:
обчислюється за такою квадратурною
формулою Гауса:
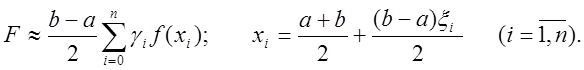
Похибка квадратурної формули Гауса має вигляд
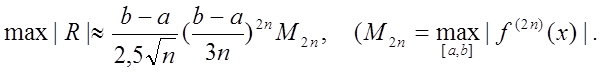
Зауважимо,
що, починаючи з ![]() , і вузли, і ваги є
ірраціональними числами, а кінці a і b ніколи не
входять до вузлів.
, і вузли, і ваги є
ірраціональними числами, а кінці a і b ніколи не
входять до вузлів.
Іншими прикладами квадратурних формул типу Гауса є формули Чебишева, Ерміта.
7.2.1 Квадратурна формула Чебишева
Візьмемо
за основу формулу 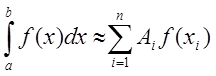 і будемо вважати всі
квадратурні коефіцієнти однаковими:
і будемо вважати всі
квадратурні коефіцієнти однаковими: ![]() . Тоді
. Тоді
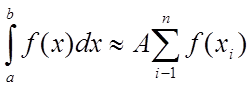 . (7.10)
. (7.10)
Параметри
![]() виберемо так, щоб формула
виберемо так, щоб формула 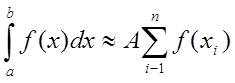 була точною для всіх поліномів степеня не
вище за
була точною для всіх поліномів степеня не
вище за ![]() При цьому достатньо розглянути функції
При цьому достатньо розглянути функції ![]()
Для
![]() маємо
маємо 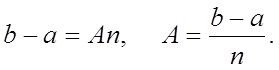
Покладаючи
в 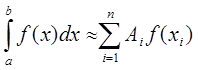
![]() приходимо до системи
нелінійних рівнянь для визначення квадратурних вузлів
приходимо до системи
нелінійних рівнянь для визначення квадратурних вузлів ![]()
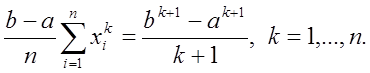
Отримана
квадратурна формула називається формулою Чебишева. Зокрема при ![]()
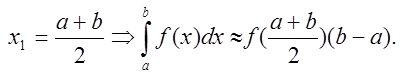
Стійкість квадратурних формул характеризує їх чутливість до різного роду похибок. Вона безпосередньо пов'язана з поняттям збіжності квадратурних формул.
Квадратурна
формула буде збіжною за умови, що залишок ![]() при
при ![]() .
.
Крім похибки,
що виникає внаслідок відкидання залишкового члена (похибки методу), виникає похибка, зумовлена виконанням дій з
наближеними числами (у процесі обчислень майже завжди доводиться мати справу з наближеними значеннями ![]() , в яких правильні тільки кілька
значущих цифр). Нехай, наприклад, всі
значення
, в яких правильні тільки кілька
значущих цифр). Нехай, наприклад, всі
значення ![]() обчислені
наближено, причому абсолютні похибки їх не
перевищують числа
обчислені
наближено, причому абсолютні похибки їх не
перевищують числа ![]()
![]() .
Обчисливши за допомогою наближених значень
.
Обчисливши за допомогою наближених значень ![]() квадратурну суму
квадратурну суму 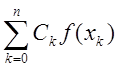 при точних значеннях
при точних значеннях ![]() , дістанемо похибку
, дістанемо похибку
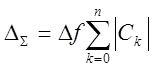 . (7.11)
. (7.11)
Це неусувна похибка квадратурної формули.
Отже, якщо сума 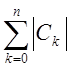 велика,
то навіть незначні похибки в значеннях
велика,
то навіть незначні похибки в значеннях ![]() можуть призвести до великої
похибки в наближеному значенні інтеграла.
Тому практичну цінність мають лише такі квадратурні формули, для яких
сума
можуть призвести до великої
похибки в наближеному значенні інтеграла.
Тому практичну цінність мають лише такі квадратурні формули, для яких
сума 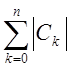 невелика.
Якщо квадратурна формула точна для
невелика.
Якщо квадратурна формула точна для ![]() , то неважко встановити
умову, за якої сума
, то неважко встановити
умову, за якої сума 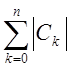 набуває
найменших значень. Справді, формула точна для
набуває
найменших значень. Справді, формула точна для ![]() тоді й
тільки тоді, коли
тоді й
тільки тоді, коли 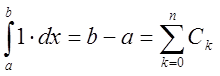 . З останнього випливає,
що
. З останнього випливає,
що 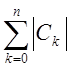 матиме
найменше значення, коли всі
матиме
найменше значення, коли всі ![]() будуть
додатні. Тому квадратурні формули з додатними коефіцієнтами використовуються найчастіше.
будуть
додатні. Тому квадратурні формули з додатними коефіцієнтами використовуються найчастіше.
Отже, повна похибка чисельного інтегрування дорівнює сумі трьох похибок: похибки методу, неусувної похибки ![]() та заключної похибки округлення результату
та заключної похибки округлення результату ![]() .
.
Існує можливість оцінити похибку квадратурної формули до початку розв’язання задачі. Така оцінка називається апріорною. Оцінка похибки після розв’язання задачі називається апостеріорною.
Розглянемо апріорну оцінку похибки
квадратурної формули Симпсона. Ця похибка графічно визначається сумою площ між
кривою ![]() та інтерполяційним поліномом Лагранжа
та інтерполяційним поліномом Лагранжа ![]() (дивись рисунок 7.2). Залишок найпростішої
формули Симпсона
(дивись рисунок 7.2). Залишок найпростішої
формули Симпсона 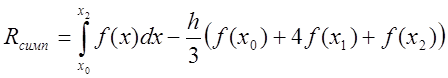 . Його можна розглядати як
функцію від кроку
. Його можна розглядати як
функцію від кроку ![]()
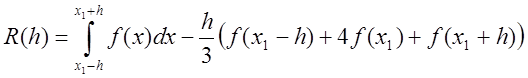 .
.
Оскільки функція ![]() ,
то:
,
то:
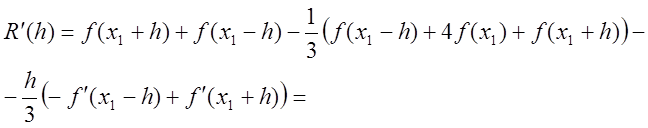
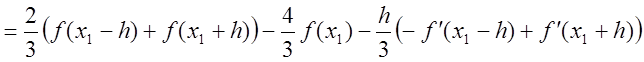 ;
;
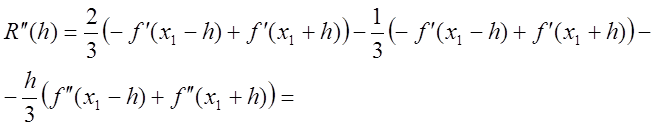
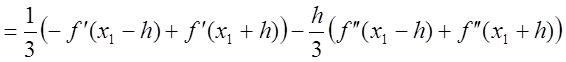 ;
;
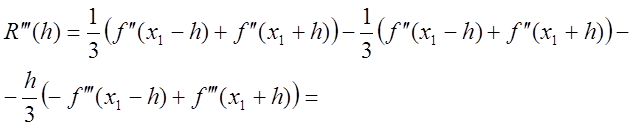
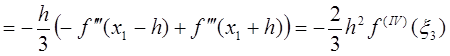 ,
,![]() ;
;
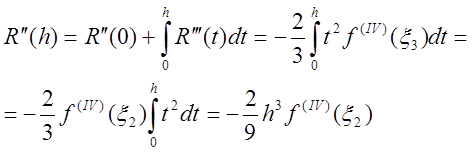 ,
,![]() ;
;
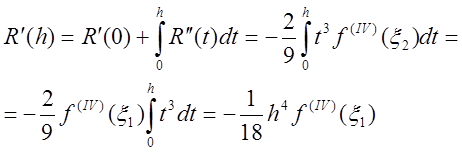 ,
,![]() ;
;
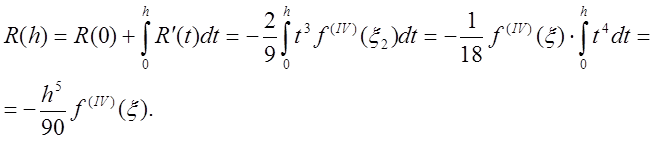 .
.
Залишковий член загальної формули Симпсона
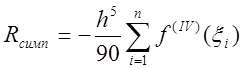 . (7.12)
. (7.12)
Оскільки ![]() –
неперервна на
–
неперервна на ![]() функція, то знайдеться така
точка
функція, то знайдеться така
точка ![]() , що
, що 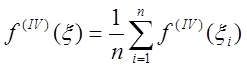
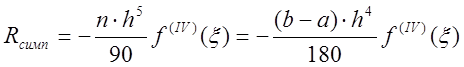 .
.
Оцінка похибки квадратурних формул часто
виявляється малоефективною через труднощі, що виникають при знаходженні
похідної підінтегральної функції ![]() :
: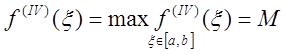 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.