Для
одержання заданої точності ![]() у разі К-кратного інтеграла сітковим
(різницевим) методом потрібно виконати близько
у разі К-кратного інтеграла сітковим
(різницевим) методом потрібно виконати близько 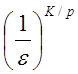 обчислень
підінтегральної функції, де р – порядок точності сіткової формули.
обчислень
підінтегральної функції, де р – порядок точності сіткової формули.
Отже,
якщо 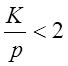 , вигідні сіткові методи, якщо ж
, вигідні сіткові методи, якщо ж 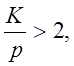 то вигідний метод Монте-Карло. Так, за
р=2 тривимірний інтеграл обчислюють сітковими методами, а при K=5 – методом Монте-Карло.
то вигідний метод Монте-Карло. Так, за
р=2 тривимірний інтеграл обчислюють сітковими методами, а при K=5 – методом Монте-Карло.
Розглянемо
інтеграл по k-вимірній області, яка розбита сіткою на комірки (Рис.
7.4). Його можна обчислити послідовним інтегруванням: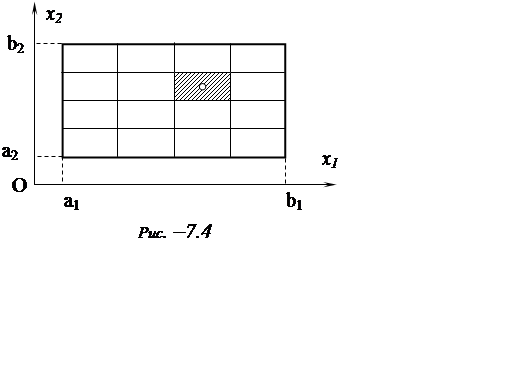
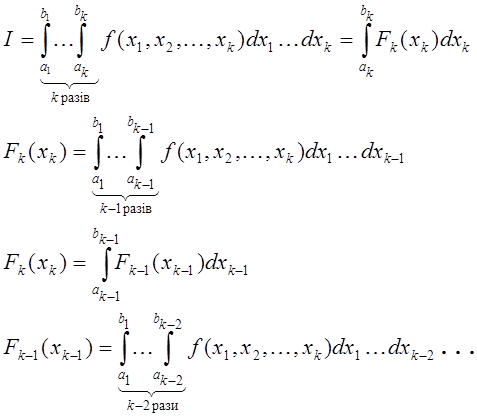
Кожний однократний інтеграл легко обчислюється на даній сітці за квадратурними формулами типу
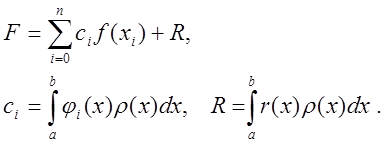
Послідовне інтегрування в усіх напрямках приводить до кубатурних формул, які є прямим добутком одновимірних квадратурних формул:
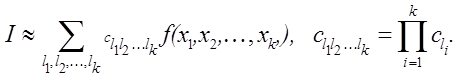 (7.20)
(7.20)
Наприклад, при k=2,
якщо по кожному напрямку обрана узагальнена формула трапецій, а сітка
рівномірна, то ваги кубатурної формули дорівнюють 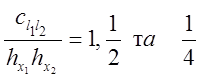 відповідно
для внутрішніх, граничних і кутових вузлів сітки. Легко показати, що для двічі
неперервно диференційованих функцій ця формула має другий порядок точності, і
до неї застосуємо метод Рунге-Ромберга.
відповідно
для внутрішніх, граничних і кутових вузлів сітки. Легко показати, що для двічі
неперервно диференційованих функцій ця формула має другий порядок точності, і
до неї застосуємо метод Рунге-Ромберга.
Взагалі
для різних напрямків можна використати квадратурні формули різних порядків
точності ![]() . Тоді головний член похибки має вигляд
. Тоді головний член похибки має вигляд
![]()
Бажано для всіх напрямків використовувати квадратурні формули однакового порядку точності.
Можна підібрати ваги й положення ліній сітки так, щоб одновимірна квадратурна формула була точною для многочлена максимального степеня, тобто була б формулою Гауса. Тоді для випадку k=2:
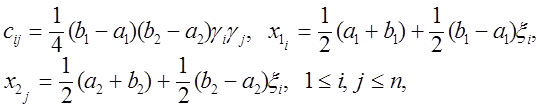 (7.21)
(7.21)
де ![]() -нулі многочленів Лежандра й відповідні
ваги. Ці формули розраховані на функції високої гладкості й дають для них
більшу економію за кількістю вузлів у порівнянні з простішими формулами.
-нулі многочленів Лежандра й відповідні
ваги. Ці формули розраховані на функції високої гладкості й дають для них
більшу економію за кількістю вузлів у порівнянні з простішими формулами.
Метод
послідовного інтегрування можна застосовувати до області довільної форми,
наприклад, із криволінійною границею. Розглянемо цей випадок при K=2.
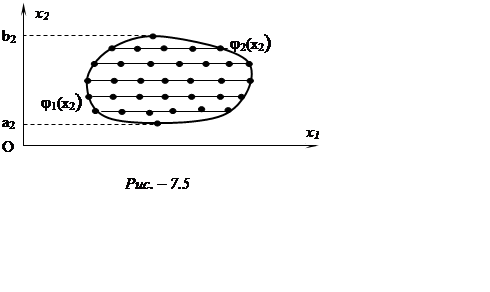
Для цього проведемо через область хорди, паралельні осі ![]() ,
і на них уведемо вузли, розміщені на кожній хорді так, як нам потрібно (рис.
7.5). Представимо інтеграл у вигляді
,
і на них уведемо вузли, розміщені на кожній хорді так, як нам потрібно (рис.
7.5). Представимо інтеграл у вигляді
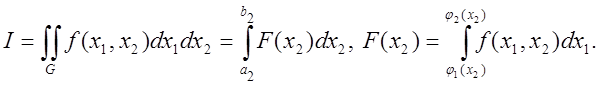
Спочатку
обчислимо інтеграл по ![]() уздовж кожної хорди за будь-якою
одномірною квадратурною формулою, використовуючи введені вузли. Потім обчислимо
інтеграл по
уздовж кожної хорди за будь-якою
одномірною квадратурною формулою, використовуючи введені вузли. Потім обчислимо
інтеграл по ![]() ; тут вузлами будуть служити проекції хорд
на вісь ординат.
; тут вузлами будуть служити проекції хорд
на вісь ординат.
При
обчисленні інтеграла по ![]() є одна особливість.
Якщо область обмежена гладкою кривою, то при
є одна особливість.
Якщо область обмежена гладкою кривою, то при ![]() довжина
хорди прямує до нуля не лінійно, а як
довжина
хорди прямує до нуля не лінійно, а як ![]() ;
виходить, поблизу цієї точки
;
виходить, поблизу цієї точки ![]() . Те саме буде при
. Те саме буде при ![]() . Тому інтегрувати безпосередньо
. Тому інтегрувати безпосередньо ![]() за формулами високого порядку точності не
має сенсу. Доцільно виділити з
за формулами високого порядку точності не
має сенсу. Доцільно виділити з ![]() основну особливість у
вигляді ваги
основну особливість у
вигляді ваги ![]() , якій відповідають ортогональні
многочлени Чебишева другого роду.
, якій відповідають ортогональні
многочлени Чебишева другого роду.
Тоді друге інтегрування виконується за формулами Гауса
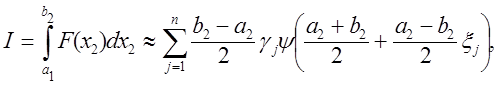 (7.22)
(7.22)
 де
де 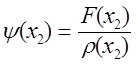 , а
, а 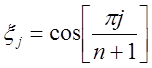 й
й ![]() -нулі й ваги многочленів Чебишева другого
роду.
-нулі й ваги многочленів Чебишева другого
роду.
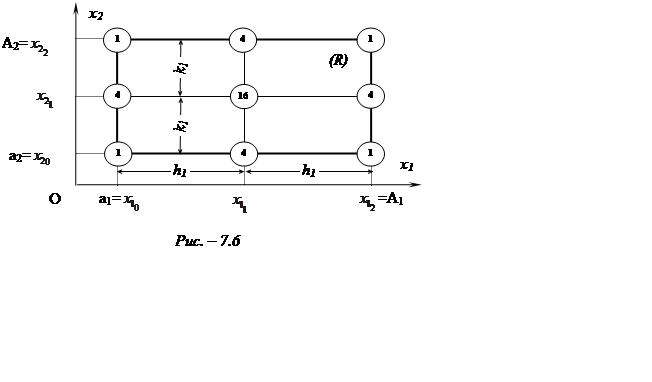
Нехай областю інтегрування є K-вимірний просторовий паралелепіпед ![]() (рис.7.6), сторони якого паралельні осям
координат. Кожний із проміжків
(рис.7.6), сторони якого паралельні осям
координат. Кожний із проміжків ![]() розіб'ємо навпіл
точками:
розіб'ємо навпіл
точками:
![]() , де
, де 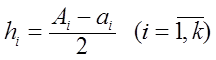 .
.
Усього,
таким чином, одержимо ![]() точок сітки. Маємо
точок сітки. Маємо
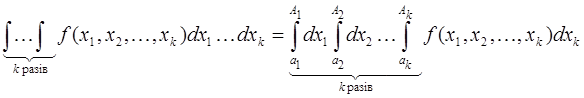 . (7.23)
. (7.23)
Знаходимо K-вимірний інтеграл, обчислюючи кожний внутрішній інтеграл за квадратурною формулою Симпсона на відповідному відрізку. Проведемо повністю всі обчислення для випадку K=2:
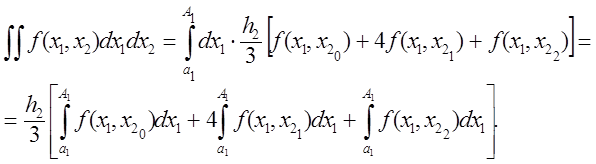
Застосовуючи до кожного інтеграла знову формулу Симпсона, одержимо:
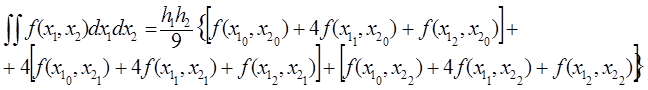 ,
,
або
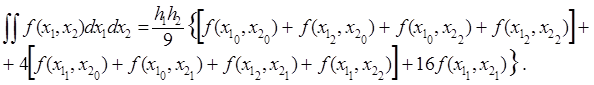 (7.24)
(7.24)
Формулу (7.24) будемо називати кубатурною формулою Симпсона. Отже,
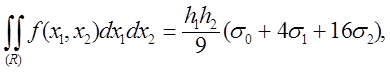 (7.25)
(7.25)
де ![]() – сума значень підінтегральної функції
– сума значень підінтегральної функції ![]() у
вершинах прямокутника
у
вершинах прямокутника ![]() ,
, ![]() – сума значень
– сума значень ![]() у серединах сторін прямокутника
у серединах сторін прямокутника ![]() ,
, ![]() –
значення функції
–
значення функції ![]() в центрі прямокутника
в центрі прямокутника ![]() . Кратності цих значень
позначені на рис. 7.6.
. Кратності цих значень
позначені на рис. 7.6.
Якщо
розміри просторового паралелепіпеда ![]() великі, то для збільшення
точності кубатурної формули область
великі, то для збільшення
точності кубатурної формули область ![]()
 розбивають на систему
паралелепіпедів, до кожного з яких застосовують кубатурну формулу Симпсона.
розбивають на систему
паралелепіпедів, до кожного з яких застосовують кубатурну формулу Симпсона.
Знову розглянемо випадок K=2. Покладемо, що сторони прямокутника ![]() ми розділили відповідно на
ми розділили відповідно на ![]() й
й ![]() однакових
частин; у результаті вийшла відносно велика мережа
однакових
частин; у результаті вийшла відносно велика мережа ![]() прямокутників
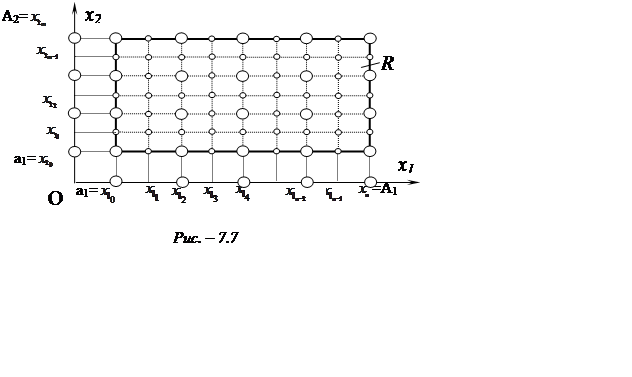
(на рис. 7.7 вершини цих прямокутників відзначені більшими кружками). Кожний із
цих прямокутників, у свою чергу, розділимо на чотири однакові частини. Вершини
цієї останньої дрібної мережі прямокутників візьмемо за вузли
прямокутників
(на рис. 7.7 вершини цих прямокутників відзначені більшими кружками). Кожний із
цих прямокутників, у свою чергу, розділимо на чотири однакові частини. Вершини
цієї останньої дрібної мережі прямокутників візьмемо за вузли ![]() кубатурної формули.
кубатурної формули.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.