Логопериодические вибраторные антенны: Учебное пособие, страница 19

В последние годы появился ряд работ [52], [53], где используются другие варианты функции Грина [54] неограниченного пространства, в которых электрический вибратор заменяется идеально проводящей трубкой. Эти представления функций Грина позволяют учесть конечную ширину зазора в точках питания вибраторов, в то время как обычно этот зазор предполагается нулевым.

Эти разложения функций Грина используются для построения сингулярных ИУ относительно производной тока вибратора по продольной координате.

Использование этих функций Грина в наших расчётах не представляется возможным, причём не столько за счёт математических сложностей, сколько за счёт резкого (на несколько порядков) увеличения затрат машинного времени.

В большей части математических выражений для анализа ЛПВА используются электрические размеры, то есть линейные размеры, умноженные на коэффициент фазы, равный в свободном пространстве . В этом случае любой линейный размер выражается через длину волны , а отрезок длиною  будет равен . Электрические размеры удобнее линейных, так как позволяют быстрее найти ошибки в математических выкладках и несколько сокращают время вычислений. Поэтому заменим линейные размеры в пределах интегрирования в выражениях (1.28), (1.29) на электрические размеры

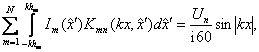                     (1.31)

где

; .

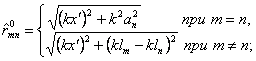В правой части (1.31) находятся неизвестные клеммные напряжения. Их следует выразить через значения клеммных токов . Заметим, что напряжения на вибраторах равны напряжениям на клеммах распределительного фидера. Введя для распределительного фидера матрицу , получим

.                                         (1.32)

При описании параметров распределительного фидера была определена матрица . Матрицу  определим как обращение матрицы , то есть .

В выражении (1.32)  – токи, втекающие на клеммы распределительного фидера, которые просто связаны с токами , втекающими на клеммы вибраторов,

                           (1.33)

откуда

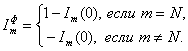                             (1.34)

С учётом (1.32), (1.33) и (1.34) преобразуем (1.31) к виду:

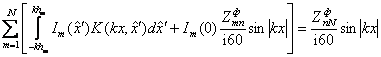.        (1.35)

Для нахождения тока , текущего по m-му вибратору, представим его в соответствии с методом моментов в виде ряда по некоторым базисным функциям :

,                                           (1.36)

где  – неизвестные коэффициенты разложения, – количество гармоник тока.

Уравнение (1.36) справедливо в пределах n-го вибратора, то есть при . Потребуем, чтобы оно выполнялось в дискретных точках . Тогда подставляя (1.36) в (1.35), получим окончательную систему из  линейных алгебраических уравнений, решение которой определяет искомые коэффициенты :