Логопериодические вибраторные антенны: Учебное пособие, страница 16

Математической моделью трубки электрического тока, текущего только вдоль оси вибратора, является нить тока с плотностью линейного тока (часто называемого током) , совмещённая с осью вибратора [50], причём  т.е. ток равен нулю на концах плеч вибратора. Так как вибратор симметричный, то . Это краевые условия, используемые для определения тока. В случае вибратора цилиндрической формы . Поэтому

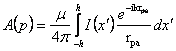,                               (1.19)

где  т.е. считается, что точка интегрирования находится на цилиндрической поверхности плеч вибратора [50]. Для сокращения записи индексы при  ниже опускаем, т.е.

Для составления интегрального уравнения тока учтём, что  является вторичным током, возбуждаемым под воздействием стороннего ЭМ поля с векторами напряжённостей  (при ), наводимого источником идеальной электродвижущей силы с напряжением –U_o, и ЭМ полем с векторами напряжённостей  в окружающем вибратор пространстве. Это ЭМ поле порождается самим вторичным током

Так как  то в зазоре

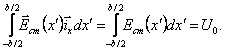
При идеальной проводимости плеч вибратора касательная к поверхности S составляющая  вектора  должна обращаться в нуль на S. В зазоре эта составляющая равна  значит, граничным условием при  является

Учитывая, что , с помощью (1.17) определяем :

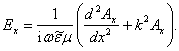
Подставляя это выражение в граничное условие, имеем при

                  (1.20)

Решение этого неоднородного обыкновенного дифференциального уравнения второго порядка может быть получено методом функций Грина или методом вариации постоянных. Применяем метод функций Грина. Для этого на интервале , на концах которого не поставлены краевые условия, определим функцию Грина  уравнения

где .

Записывая два решения на интервалах  и , учитывая равенство решений и разрыв первых производных этих решений при  [51], находим

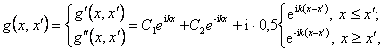
где коэффициенты С₁, С₂ определяются краевыми условиями при .

Решение уравнения (1.20) получаем с помощью последнего выражения.

           (1.21)